01. 单车预测器：我的第一个PyTorch神经网络

首页
/ 深度学习 / 正文

1. 期望目标：

① Python作图实现数据可视化

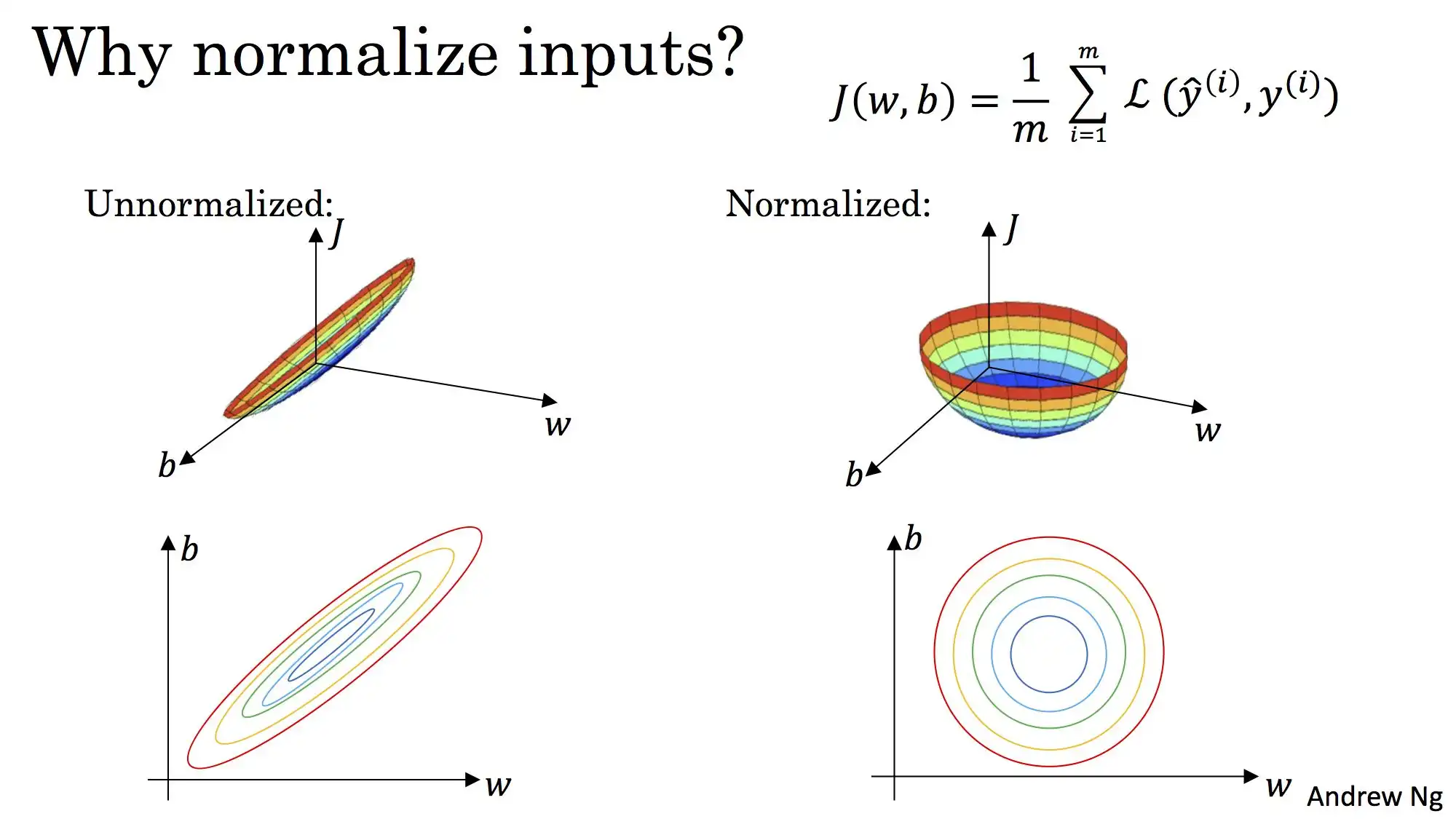
② 从训练结果观察输入变量归一化的好处

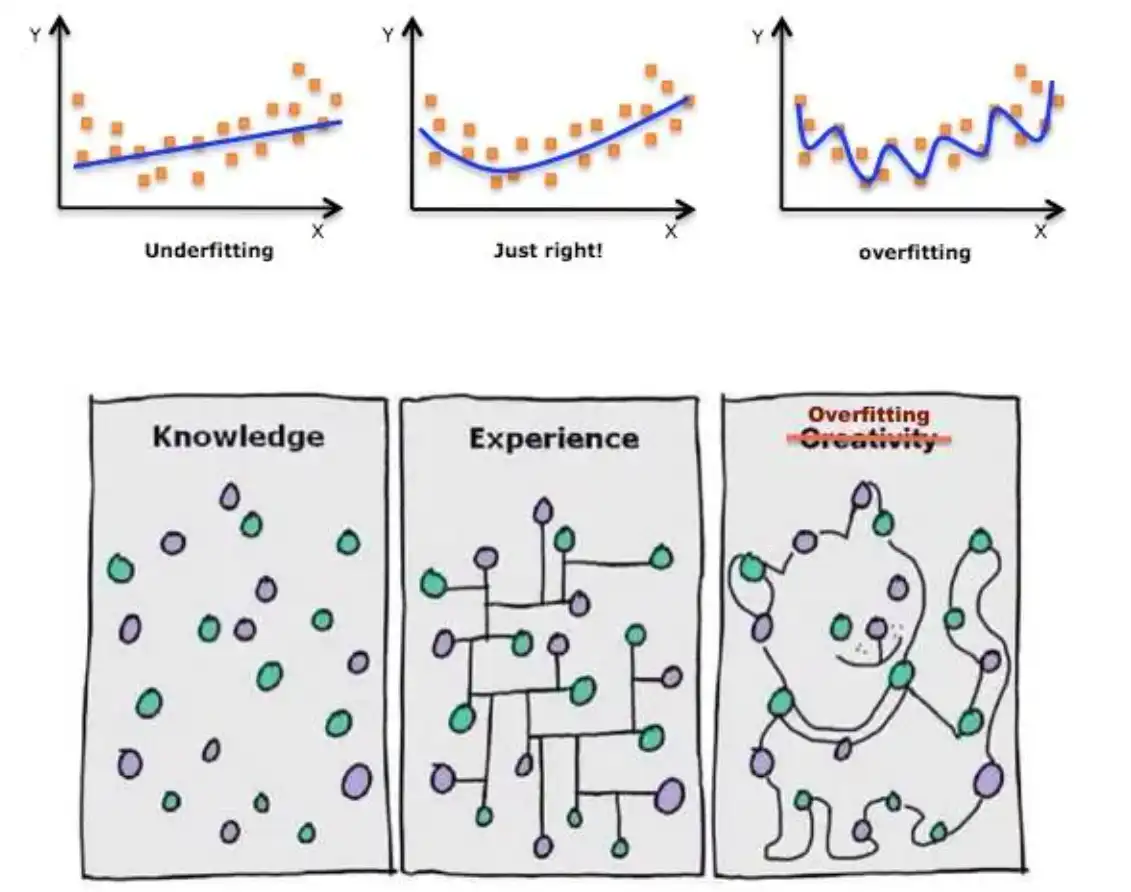
③ 从预测效果发现过拟合的弊端

2. 下载数据集 & 数据集简介

→国外的共享单车公开数据集官网
→需要用到的上述数据'hour.csv'国内镜像直接下载

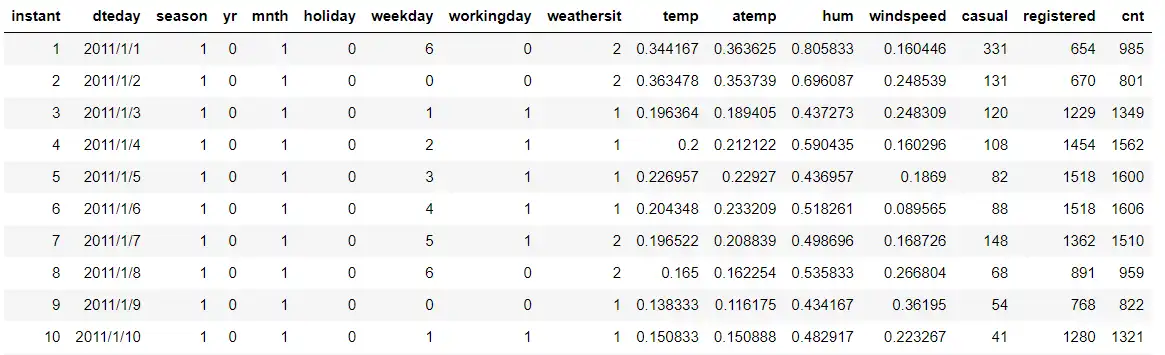
  为避免商业纠纷，我们采用国外公开数据集(Capital Bikeshare)，可直接点击上方的链接下载。截取其中的前11行数据如下图所示：

bGiYGV.png

其中各数据列信息对应关系如下：

列名信息列名信息列名信息
instant记录索引dteday日期season季节
yr年份mnth月份hr小时
holiday是否节假日weekday星期workingday周末或假日为0
weathersit天气temp温度atemp标准化感受温度
hum湿度windspeed风速casual临时用户数
registered注册用户数cnt用户数

  由于本例是搭建的第一个PyTorch神经网络，为了方便起见，我们用小时数x = 1, 2, 3, ··· 50 来预测用户数cnt的变化。

3. 单车预测器1.0

  据神经网络的函数叠加原理，只要变换参数组合，我们就可以用单一隐含层中有两个神经元的简单网络拟合出任意具有单峰的曲线，那么，如果有4个、6个隐含层神经元，我们就可以拟合出具有双峰、三峰的曲线。我们接下来要拟合的数据具有多个波峰，那么我们想搭建单一隐含层的神经网络所需的隐含层神经元个数就可以由要拟合的曲线波峰数决定。

3-1. 准备数据 & 作图展示

导入函数包：

# 导入本例中用到的所有函数包
import numpy as np
import pandas as pd
import torch
from torch.autograd import Variable
import matplotlib.pyplot as plt

从本地导入'hour.csv'数据：

data_path = './hour.csv'
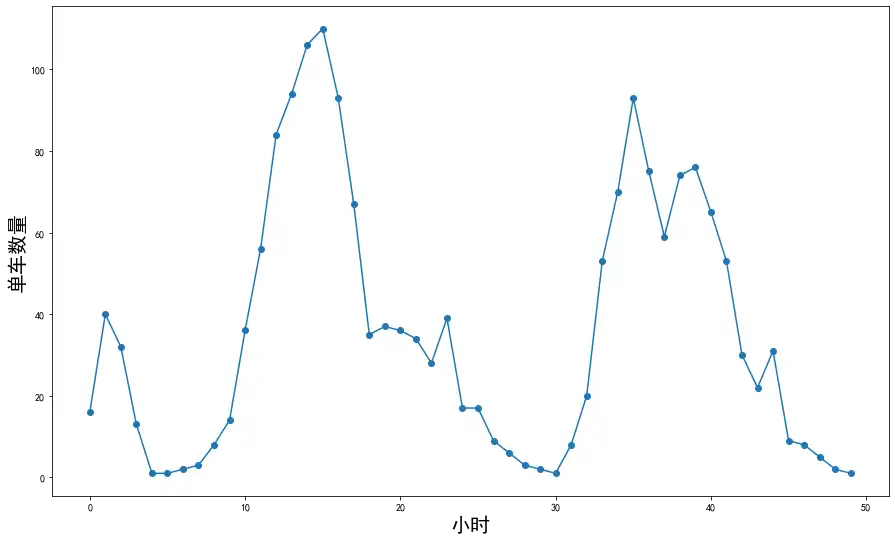
rides = pd.read_csv(data_path) # rides 为一个 dataframe 对象

截取前50条数据并作图显示：

counts = rides['cnt'][:50]# 截取前50条数据
x = np.arange(len(counts))# 获取变量x——0到49
y = np.array(counts)# 单车数量为y,————————此时y为(1, 50)

plt.figure(figsize = (15, 9))# 设定绘图窗口大小
plt.plot(x, y, 'o-')# 绘制原始数据

# 显示中文
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False

plt.xlabel('小时', size = 20)
plt.ylabel('单车数量', size = 20)

bGi1Vs.png

  从上图发现，这些数据点大致形成了5个波峰，因此我们采用10个隐含层神经元进行拟合即可。接下来，我们要选取一个平均损失函数来表示拟合曲线与真实数据之间的差异，即：

$$ L = \frac{1}{N}\sum_i^N(y_i-\hat y_i)^2 $$

3-2. 搭建神经网络

# 输入变量0, 1, 2, ... 49这样的一维数组
x = Variable(torch.FloatTensor(np.arange(len(counts), dtype = float)))
# 输出变量，它是从数据counts中读取的每一时刻的单车数，共50个数据点的一维数组，作为标准答案
y = Variable(torch.FloatTensor(np.array(counts, dtype = float).reshape(50, 1)))
# 此时y为(50, 1)

sz = 10# 设置隐含层神经元的数量
# 初始化输入层到隐含层的权重矩阵，尺寸(1, 10)
weights = Variable(torch.randn(1, sz), requires_grad = True)
# 初始化隐含层节点的偏置向量，尺寸为10的一维向量
biases = Variable(torch.randn(sz), requires_grad = True)
# 初始化从隐含层到输出层的权重矩阵，尺寸(10, 1)
weights2 = Variable(torch.randn(sz, 1), requires_grad = True)

3-3. 迭代训练神经网络

learning_rate = 0.0001# 设置学习率
losses = []# 该数组记录每一次迭代的损失函数值，以方便后续绘图
for i in range(1000000):   
    # 从输入层到隐含层的计算
    hidden = x.expand(sz, len(x)).t() * weights.expand(len(x), sz) + biases.expand(len(x), sz)
    # 此时hidden变量的尺寸是：(50, 10)，即50个数据点，10个隐含层神经元
    
    # 将sigmoid函数作用在隐含层的每一个神经元上
    hidden = torch.sigmoid(hidden)
    # 隐含层输出到输出层，计算得到最终预测
    predictions = hidden.mm(weights2)
    # 此时predictions的尺寸为：(50, 1)，即50个数据点的预测数值
    
    # 通过与数据中的标准答案y作比较，计算均方误差
    loss = torch.mean((predictions - y) ** 2)
    
    # 此时loss为一个标量，即1个数
    losses.append(loss)
    
    # 每隔10000个周期打印一下损失函数数值
    if i % 10000 == 0:
        print('loss', loss)
        
    ####################################################################
    # 接下来开始梯度下降算法，将误差反向传播
    loss.backward()# 对损失函数进行梯度反传    
        
    # 利用上一步计算中得到的weights, biases 等梯度信息更新weights或biases的数值
    weights.data.add_(- learning_rate * weights.grad.data)
    biases.data.add_(- learning_rate * biases.grad.data)
    weights2.data.add_(- learning_rate * weights2.grad.data)
    
    # 清空所有变量的梯度值
    weights.grad.data.zero_()
    biases.grad.data.zero_()
    weights2.grad.data.zero_()

训练过程中每次输出的平均损失函数值如下：

loss tensor(2048.0120, grad_fn=<MeanBackward0>)
loss tensor(938.6091, grad_fn=<MeanBackward0>)
loss tensor(910.8022, grad_fn=<MeanBackward0>)
loss tensor(897.9393, grad_fn=<MeanBackward0>)
loss tensor(890.0558, grad_fn=<MeanBackward0>)
loss tensor(883.3086, grad_fn=<MeanBackward0>)
loss tensor(861.1828, grad_fn=<MeanBackward0>)
loss tensor(805.1549, grad_fn=<MeanBackward0>)
loss tensor(740.3658, grad_fn=<MeanBackward0>)
loss tensor(690.6590, grad_fn=<MeanBackward0>)
loss tensor(652.1323, grad_fn=<MeanBackward0>)
loss tensor(621.0927, grad_fn=<MeanBackward0>)
loss tensor(595.6832, grad_fn=<MeanBackward0>)
loss tensor(574.7310, grad_fn=<MeanBackward0>)
loss tensor(557.3751, grad_fn=<MeanBackward0>)
loss tensor(542.9405, grad_fn=<MeanBackward0>)
loss tensor(530.8903, grad_fn=<MeanBackward0>)
loss tensor(520.7909, grad_fn=<MeanBackward0>)
loss tensor(512.2971, grad_fn=<MeanBackward0>)
loss tensor(505.1256, grad_fn=<MeanBackward0>)
loss tensor(499.0471, grad_fn=<MeanBackward0>)
loss tensor(493.8675, grad_fn=<MeanBackward0>)
loss tensor(489.4166, grad_fn=<MeanBackward0>)
loss tensor(485.5419, grad_fn=<MeanBackward0>)
loss tensor(482.1412, grad_fn=<MeanBackward0>)
loss tensor(479.1540, grad_fn=<MeanBackward0>)
loss tensor(476.5240, grad_fn=<MeanBackward0>)
loss tensor(474.2075, grad_fn=<MeanBackward0>)
loss tensor(472.1636, grad_fn=<MeanBackward0>)
loss tensor(470.3613, grad_fn=<MeanBackward0>)
loss tensor(468.7662, grad_fn=<MeanBackward0>)
loss tensor(467.3491, grad_fn=<MeanBackward0>)
loss tensor(466.0990, grad_fn=<MeanBackward0>)
loss tensor(464.9821, grad_fn=<MeanBackward0>)
loss tensor(463.9947, grad_fn=<MeanBackward0>)
loss tensor(463.1052, grad_fn=<MeanBackward0>)
loss tensor(462.3118, grad_fn=<MeanBackward0>)
loss tensor(461.5901, grad_fn=<MeanBackward0>)
loss tensor(460.9363, grad_fn=<MeanBackward0>)
loss tensor(460.3407, grad_fn=<MeanBackward0>)
loss tensor(459.7904, grad_fn=<MeanBackward0>)
loss tensor(459.2776, grad_fn=<MeanBackward0>)
loss tensor(458.7991, grad_fn=<MeanBackward0>)
loss tensor(458.3565, grad_fn=<MeanBackward0>)
loss tensor(457.9320, grad_fn=<MeanBackward0>)
loss tensor(457.5314, grad_fn=<MeanBackward0>)
loss tensor(457.1586, grad_fn=<MeanBackward0>)
loss tensor(456.7987, grad_fn=<MeanBackward0>)
loss tensor(456.4561, grad_fn=<MeanBackward0>)
loss tensor(456.1297, grad_fn=<MeanBackward0>)
loss tensor(455.8208, grad_fn=<MeanBackward0>)
loss tensor(455.5273, grad_fn=<MeanBackward0>)
loss tensor(455.2435, grad_fn=<MeanBackward0>)
loss tensor(454.9713, grad_fn=<MeanBackward0>)
loss tensor(454.7216, grad_fn=<MeanBackward0>)
loss tensor(454.4871, grad_fn=<MeanBackward0>)
loss tensor(454.2638, grad_fn=<MeanBackward0>)
loss tensor(454.0493, grad_fn=<MeanBackward0>)
loss tensor(453.8435, grad_fn=<MeanBackward0>)
loss tensor(453.6457, grad_fn=<MeanBackward0>)
loss tensor(453.4618, grad_fn=<MeanBackward0>)
loss tensor(453.2882, grad_fn=<MeanBackward0>)
loss tensor(453.1236, grad_fn=<MeanBackward0>)
loss tensor(452.9684, grad_fn=<MeanBackward0>)
loss tensor(452.8231, grad_fn=<MeanBackward0>)
loss tensor(452.6828, grad_fn=<MeanBackward0>)
loss tensor(452.5495, grad_fn=<MeanBackward0>)
loss tensor(452.4209, grad_fn=<MeanBackward0>)
loss tensor(452.2989, grad_fn=<MeanBackward0>)
loss tensor(452.1870, grad_fn=<MeanBackward0>)
loss tensor(452.0817, grad_fn=<MeanBackward0>)
loss tensor(451.9794, grad_fn=<MeanBackward0>)
loss tensor(451.8820, grad_fn=<MeanBackward0>)
loss tensor(451.7878, grad_fn=<MeanBackward0>)
loss tensor(451.6990, grad_fn=<MeanBackward0>)
loss tensor(451.6144, grad_fn=<MeanBackward0>)
loss tensor(451.5352, grad_fn=<MeanBackward0>)
loss tensor(451.4583, grad_fn=<MeanBackward0>)
loss tensor(451.3846, grad_fn=<MeanBackward0>)
loss tensor(451.3141, grad_fn=<MeanBackward0>)
loss tensor(451.2463, grad_fn=<MeanBackward0>)
loss tensor(451.1818, grad_fn=<MeanBackward0>)
loss tensor(451.1194, grad_fn=<MeanBackward0>)
loss tensor(451.0609, grad_fn=<MeanBackward0>)
loss tensor(451.0052, grad_fn=<MeanBackward0>)
loss tensor(450.9518, grad_fn=<MeanBackward0>)
loss tensor(450.9005, grad_fn=<MeanBackward0>)
loss tensor(450.8508, grad_fn=<MeanBackward0>)
loss tensor(450.8034, grad_fn=<MeanBackward0>)
loss tensor(450.7570, grad_fn=<MeanBackward0>)
loss tensor(450.7128, grad_fn=<MeanBackward0>)
loss tensor(450.6700, grad_fn=<MeanBackward0>)
loss tensor(450.6284, grad_fn=<MeanBackward0>)
loss tensor(450.5893, grad_fn=<MeanBackward0>)
loss tensor(450.5510, grad_fn=<MeanBackward0>)
loss tensor(450.5133, grad_fn=<MeanBackward0>)
loss tensor(450.4772, grad_fn=<MeanBackward0>)
loss tensor(450.4421, grad_fn=<MeanBackward0>)
loss tensor(450.4076, grad_fn=<MeanBackward0>)
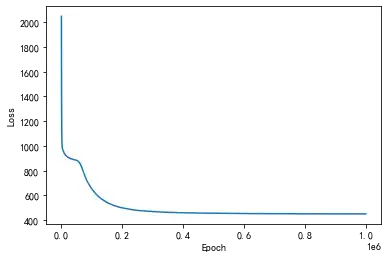
loss tensor(450.3736, grad_fn=<MeanBackward0>)

平均损失函数值随训练次数的变化图如下：

plt.plot(losses)
plt.xlabel('Epoch')
plt.ylabel('Loss')

​
bGiMrQ.png

3-4. 绘制预测曲线

x_data = x.data.numpy()
plt.figure(figsize = (10, 7))
xplot, = plt.plot(x_data, y.data.numpy(), 'o')# 绘制原始数据
yplot, = plt.plot(x_data, predictions.data.numpy())# 绘制拟合数据
plt.xlabel('X')
plt.ylabel('Y')
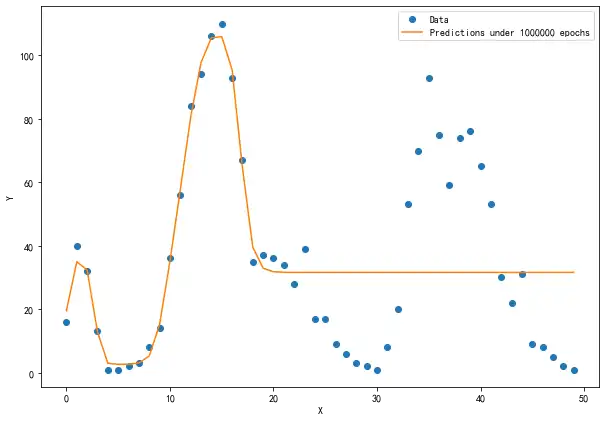
plt.legend([xplot, yplot], ['Data', 'Predictions under 1000000 epochs'])# 绘制图例
plt.show()

bGiQbj.png

  可以看到，我们预测出的曲线在前两个波峰（谷）位置比较好地拟合了数据，但是在后三个波的位置丝毫没有拟合到。这就是不进行输入数据归一化的弊端，原因如下：

bZcw1e.png

那让我们也实现一下输入归一化的效果吧：

3-5. 归一化输入后再训练

# 归一化输入
x = Variable(torch.FloatTensor(np.arange(len(counts), dtype = float) / len(counts)))
# 输出变量，它是从数据counts中读取的每一时刻的单车数，共50个数据点的一维数组，作为标准答案
y = Variable(torch.FloatTensor(np.array(counts, dtype = float).reshape(50, 1)))
# 此时y为(50, 1)

sz = 10# 设置隐含层神经元的数量
# 初始化输入层到隐含层的权重矩阵，尺寸(1, 10)
weights = Variable(torch.randn(1, sz), requires_grad = True)
# 初始化隐含层节点的偏置向量，尺寸为10的一维向量
biases = Variable(torch.randn(sz), requires_grad = True)
# 初始化从隐含层到输出层的权重矩阵，尺寸(10, 1)
weights2 = Variable(torch.randn(sz, 1), requires_grad = True)

####################################################################################
learning_rate = 0.0001# 设置学习率
losses = []# 该数组记录每一次迭代的损失函数值，以方便后续绘图
for i in range(1000000):   
    # 从输入层到隐含层的计算
    hidden = x.expand(sz, len(x)).t() * weights.expand(len(x), sz) + biases.expand(len(x), sz)
    # 此时hidden变量的尺寸是：(50, 10)，即50个数据点，10个隐含层神经元
    
    # 将sigmoid函数作用在隐含层的每一个神经元上
    hidden = torch.sigmoid(hidden)
    # 隐含层输出到输出层，计算得到最终预测
    predictions = hidden.mm(weights2)
    # 此时predictions的尺寸为：(50, 1)，即50个数据点的预测数值
    
    # 通过与数据中的标准答案y作比较，计算均方误差
    loss = torch.mean((predictions - y) ** 2)
    
    # 此时loss为一个标量，即1个数
    losses.append(loss)
    
    # 每隔10000个周期打印一下损失函数数值
    if i % 10000 == 0:
        print('loss', loss)
        
    ####################################################################
    # 接下来开始梯度下降算法，将误差反向传播
    loss.backward()# 对损失函数进行梯度反传    
        
    # 利用上一步计算中得到的weights, biases 等梯度信息更新weights或biases的数值
    weights.data.add_(- learning_rate * weights.grad.data)
    biases.data.add_(- learning_rate * biases.grad.data)
    weights2.data.add_(- learning_rate * weights2.grad.data)
    
    # 清空所有变量的梯度值
    weights.grad.data.zero_()
    biases.grad.data.zero_()
    weights2.grad.data.zero_()

归一化训练的输出：

loss tensor(2232.1956, grad_fn=<MeanBackward0>)
loss tensor(1009.6735, grad_fn=<MeanBackward0>)
loss tensor(1008.0278, grad_fn=<MeanBackward0>)
loss tensor(1005.3194, grad_fn=<MeanBackward0>)
loss tensor(1001.0356, grad_fn=<MeanBackward0>)
loss tensor(994.4739, grad_fn=<MeanBackward0>)
loss tensor(986.0559, grad_fn=<MeanBackward0>)
loss tensor(976.5992, grad_fn=<MeanBackward0>)
loss tensor(966.7902, grad_fn=<MeanBackward0>)
loss tensor(956.7433, grad_fn=<MeanBackward0>)
loss tensor(946.3423, grad_fn=<MeanBackward0>)
loss tensor(935.5558, grad_fn=<MeanBackward0>)
loss tensor(923.3160, grad_fn=<MeanBackward0>)
loss tensor(905.6027, grad_fn=<MeanBackward0>)
loss tensor(885.6800, grad_fn=<MeanBackward0>)
loss tensor(861.9071, grad_fn=<MeanBackward0>)
loss tensor(835.2570, grad_fn=<MeanBackward0>)
loss tensor(807.2561, grad_fn=<MeanBackward0>)
loss tensor(778.8225, grad_fn=<MeanBackward0>)
loss tensor(750.4874, grad_fn=<MeanBackward0>)
loss tensor(722.9290, grad_fn=<MeanBackward0>)
loss tensor(696.1763, grad_fn=<MeanBackward0>)
loss tensor(670.1414, grad_fn=<MeanBackward0>)
loss tensor(645.4695, grad_fn=<MeanBackward0>)
loss tensor(622.5213, grad_fn=<MeanBackward0>)
loss tensor(601.4258, grad_fn=<MeanBackward0>)
loss tensor(582.1887, grad_fn=<MeanBackward0>)
loss tensor(564.6752, grad_fn=<MeanBackward0>)
loss tensor(548.6738, grad_fn=<MeanBackward0>)
loss tensor(533.7887, grad_fn=<MeanBackward0>)
loss tensor(518.5122, grad_fn=<MeanBackward0>)
loss tensor(501.2513, grad_fn=<MeanBackward0>)
loss tensor(481.9189, grad_fn=<MeanBackward0>)
loss tensor(459.4899, grad_fn=<MeanBackward0>)
loss tensor(434.0431, grad_fn=<MeanBackward0>)
loss tensor(406.7646, grad_fn=<MeanBackward0>)
loss tensor(379.0977, grad_fn=<MeanBackward0>)
loss tensor(352.1760, grad_fn=<MeanBackward0>)
loss tensor(326.6823, grad_fn=<MeanBackward0>)
loss tensor(303.0083, grad_fn=<MeanBackward0>)
loss tensor(281.3285, grad_fn=<MeanBackward0>)
loss tensor(261.6236, grad_fn=<MeanBackward0>)
loss tensor(243.8515, grad_fn=<MeanBackward0>)
loss tensor(227.8400, grad_fn=<MeanBackward0>)
loss tensor(213.4295, grad_fn=<MeanBackward0>)
loss tensor(200.4457, grad_fn=<MeanBackward0>)
loss tensor(188.7289, grad_fn=<MeanBackward0>)
loss tensor(178.1229, grad_fn=<MeanBackward0>)
loss tensor(168.4898, grad_fn=<MeanBackward0>)
loss tensor(159.7224, grad_fn=<MeanBackward0>)
loss tensor(151.7084, grad_fn=<MeanBackward0>)
loss tensor(144.2771, grad_fn=<MeanBackward0>)
loss tensor(137.1654, grad_fn=<MeanBackward0>)
loss tensor(130.4073, grad_fn=<MeanBackward0>)
loss tensor(124.3577, grad_fn=<MeanBackward0>)
loss tensor(118.8384, grad_fn=<MeanBackward0>)
loss tensor(113.7776, grad_fn=<MeanBackward0>)
loss tensor(109.0823, grad_fn=<MeanBackward0>)
loss tensor(104.7167, grad_fn=<MeanBackward0>)
loss tensor(100.6338, grad_fn=<MeanBackward0>)
loss tensor(96.8137, grad_fn=<MeanBackward0>)
loss tensor(93.2035, grad_fn=<MeanBackward0>)
loss tensor(89.7978, grad_fn=<MeanBackward0>)
loss tensor(86.5656, grad_fn=<MeanBackward0>)
loss tensor(83.5272, grad_fn=<MeanBackward0>)
loss tensor(80.6312, grad_fn=<MeanBackward0>)
loss tensor(77.8521, grad_fn=<MeanBackward0>)
loss tensor(75.2792, grad_fn=<MeanBackward0>)
loss tensor(72.8291, grad_fn=<MeanBackward0>)
loss tensor(70.5304, grad_fn=<MeanBackward0>)
loss tensor(68.4096, grad_fn=<MeanBackward0>)
loss tensor(66.3938, grad_fn=<MeanBackward0>)
loss tensor(64.5329, grad_fn=<MeanBackward0>)
loss tensor(62.7757, grad_fn=<MeanBackward0>)
loss tensor(61.1504, grad_fn=<MeanBackward0>)
loss tensor(59.6161, grad_fn=<MeanBackward0>)
loss tensor(58.2221, grad_fn=<MeanBackward0>)
loss tensor(56.9172, grad_fn=<MeanBackward0>)
loss tensor(55.7389, grad_fn=<MeanBackward0>)
loss tensor(54.6476, grad_fn=<MeanBackward0>)
loss tensor(53.6584, grad_fn=<MeanBackward0>)
loss tensor(52.7480, grad_fn=<MeanBackward0>)
loss tensor(51.9001, grad_fn=<MeanBackward0>)
loss tensor(51.1375, grad_fn=<MeanBackward0>)
loss tensor(50.4248, grad_fn=<MeanBackward0>)
loss tensor(49.7671, grad_fn=<MeanBackward0>)
loss tensor(49.1584, grad_fn=<MeanBackward0>)
loss tensor(48.6123, grad_fn=<MeanBackward0>)
loss tensor(48.1005, grad_fn=<MeanBackward0>)
loss tensor(47.6199, grad_fn=<MeanBackward0>)
loss tensor(47.1797, grad_fn=<MeanBackward0>)
loss tensor(46.7883, grad_fn=<MeanBackward0>)
loss tensor(46.4156, grad_fn=<MeanBackward0>)
loss tensor(46.0668, grad_fn=<MeanBackward0>)
loss tensor(45.7369, grad_fn=<MeanBackward0>)
loss tensor(45.4166, grad_fn=<MeanBackward0>)
loss tensor(45.1070, grad_fn=<MeanBackward0>)
loss tensor(44.8259, grad_fn=<MeanBackward0>)
loss tensor(44.5781, grad_fn=<MeanBackward0>)
loss tensor(44.3403, grad_fn=<MeanBackward0>)

  可以很明显地发现，这两次同样都是训练1000000次，而归一化模型仅仅修改了1行代码，平均损失值loss的收敛速度就变得飞快！不进行输入数据归一化时，loss值从2048下降到了450，而归一化后，loss值从2232直接下降到了44！

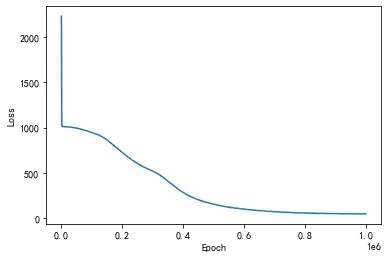
观察第二次平均损失函数值随训练次数的变化关系曲线：

plt.plot(losses)
plt.xlabel('Epoch')
plt.ylabel('Loss')

bGiKKg.png
​
作图显示拟合效果：

x_data = x.data.numpy()
plt.figure(figsize = (10, 7))
xplot, = plt.plot(x_data, y.data.numpy(), 'o')# 绘制原始数据
yplot, = plt.plot(x_data, predictions.data.numpy())# 绘制拟合数据
plt.xlabel('X')
plt.ylabel('Y')
plt.legend([xplot, yplot], ['Data', 'Predictions under 1000000 epochs'])# 绘制图例
plt.show()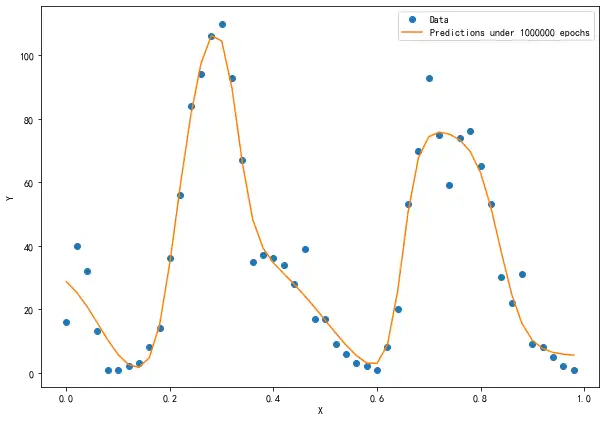

​
bGinxS.png
​
  后来改进的输入数据归一化模型非常好地拟合出了所有该有的波峰（谷），形成了一条优美的曲线。

  接下来，让我们拿起训练好的模型预测一下后50条数据，看看效果怎么样。这里需要注意的是，后50条数据的x值是51, 52, ··· ,100，同样也要除以50进行归一化。

3-6. 用归一化训练好的模型进行预测

# 要预测后50个点，因此要预测的x取值为51, 52, ..., 100，同样也要除以50
counts_predict = rides['cnt'][50:100]
# 读取待遇测的后50个数据点
x = Variable(torch.FloatTensor((np.arange(len(counts_predict), dtype = float) + len(counts)) / len(counts)))
# 读取后面50个点的y数值，不需要做归一化
y = Variable(torch.FloatTensor(np.array(counts_predict, dtype = float)))

# 用x预测y
# 从输入层到隐含层的计算
hidden = x.expand(sz, len(x)).t() * weights.expand(len(x), sz)
# 将sigmoid函数作用在隐含层的每一个神经元上
hidden = torch.sigmoid(hidden)
# 从隐含层输出到输出层，计算得到最终预测
predictions = hidden.mm(weights2)
# 计算预测数据上的损失函数
loss = torch.mean((predictions - y) ** 2)
print(loss)
tensor(6862.3838, grad_fn=<MeanBackward0>)

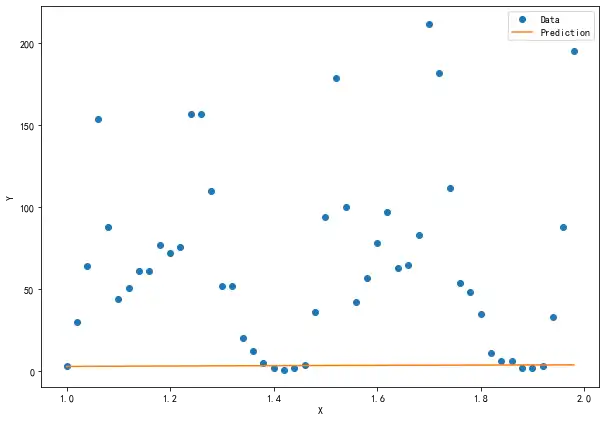
平均误差竟然达到了惊人的6862，快让我们画出来预测图看看究竟是怎么一回事：

# 将预测曲线绘制出来
x_data = x.data.numpy() #获得x包裹的数据
plt.figure(figsize = (10, 7)) #设定绘图窗口大小
xplot, = plt.plot(x_data, y.data.numpy(), 'o') #绘制原始数据
yplot, = plt.plot(x_data, predictions.data.numpy()) #绘制拟合数据
plt.xlabel('X')
plt.ylabel('Y')
plt.legend([xplot, yplot],['Data', 'Prediction']) #绘制图形
plt.show()

bGi85q.png
​
预测的数据竟然完完全全没有对上！

  那为什么我们的神经网络可以非常好地拟合已知的50个数据点，却完全不能预测出更多的数据点呢？原因就在于：过拟合。

让我们参考一下集智俱乐部图书给出的解释：

blD3VJ.png

4. 小结

Python作图实现数据可视化
数据类型：NumPy的NDarray；
作图函数包：matplotlib

输入变量归一化的好处
提升模型的收敛速度；
提升模型的回归精度

过拟合的弊端
对已知数据的拟合过度复杂；
无法预测未来

单车预测器

下一篇文章将会从实际出发，进行数据预处理、划分训练集和测试集、自动构建神经网络分批处理，实现很不错的预测未来效果······

5. 文章首图：

① Python作图：


bJPBWV.png
bJPwiq.png

② 为什么要进行输入数据标准化：


bJPaon.jpg

③ 什么是过拟合：


bJP0J0.png

本文参考书籍为：

集智俱乐部主编.《深度学习原理与pytorch实战》.人民邮电出版社.2020

输入数据归一化和过拟合的解释图来自本书，侵删。

深度学习回归
版权属于：EzXxY
本文链接：https://blog.ezxxy.work/archives/53.html
作品采用 知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议 进行许可
打赏
已经没有了
« 上一篇
02. 单车预测器：可以真正解决问题并预测未来的神经网络模型
下一篇 »
文章目录