了解到输入变量归一化的好处和引起模型过拟合的原因后,我们还需要从实际出发,进行数据预处理:类型变量的独热编码、数值变量的标准化、划分训练集和测试集;用PyTorch自带函数构建神经网络分批处理来训练真正能预测未来的神经网络模型。
1. 期望目标:
① 要对什么样的数据进行预处理
② 如何构建自动分批处理的神经网络模型
③ 不同方法预测未来数据结果对比
2. 数据预处理
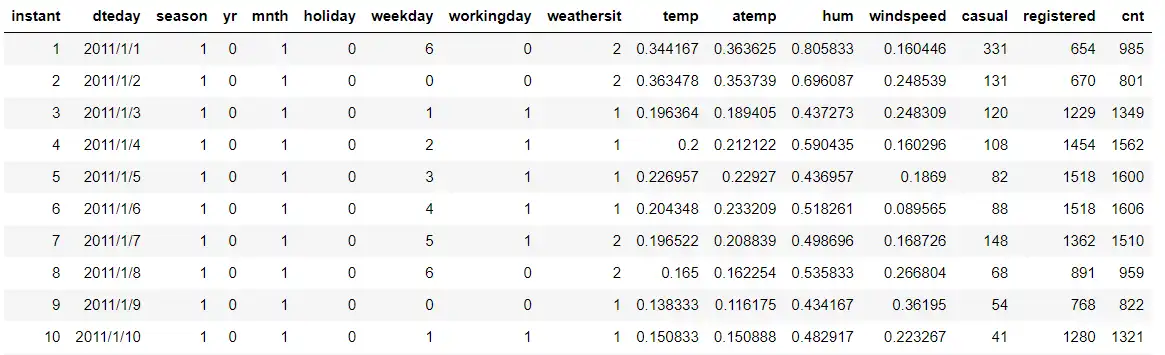
开始处理数据之前,让我们再来看一下已知的'hour.csv'数据及其各列的含义:
hour.csv部分展示:
hour.csv各列含义:
| 列名 | 信息 | 列名 | 信息 | 列名 | 信息 |
|---|---|---|---|---|---|
| instant | 记录索引 | dteday | 日期 | season | 季节 |
| yr | 年份 | mnth | 月份 | hr | 小时 |
| holiday | 是否节假日 | weekday | 星期 | workingday | 周末或假日为0 |
| weathersit | 天气 | temp | 温度 | atemp | 标准化感受温度 |
| hum | 湿度 | windspeed | 风速 | casual | 临时用户数 |
| registered | 注册用户数 | cnt | 用户数 |
可以看到,数据共17列,其中能够作为因变量的只有三列,分别为:用户数(cnt)、临时用户数(casual)和注册用户数(registered),我们可以拿3者分别作为因变量来训练模型,建模过程可以拿用户数(cnt)作为因变量举例。
剩下的14列都可以作为自变量输入,但考虑到实际问题,可以删除记录索引(instant)、日期(dtaday)、标准化感受温度(atemp)和周末或假日为0,其他为1(workingday)这四个变量。剩下的10个变量中分为了两大类——一类是无需进行处理的;另一类是需要处理的。接下来将详细说明。
② 像“是否节假日(holiday)”这样的,数值只有0或1的数据。
② 像“温度(temp)”这样数值在某一区间内可以连续变化的数据——数值变量
2-1. 类型变量的独热编码
选取的10个自变量中,类型变量有5个,分别为:“季节(season)”、“天气(weathersit)”、“月份(mnth)”、“小时(hr)”和“星期(weekday)”。如果我们要把“季节(season)”这一类型变量直接放到神经网络中,1、2、3、4的数值并不能表示信号的强度,我们需要一种转化方法——独热编码。这一编码方法实现的方式为将“季节”这1列扩展成了4列,每行可以表示一个向量,且各行向量的模长都为1,如下所示:
| 季节类型 | 独热编码 |
|---|---|
| 1 | (1,0,0,0) |
| 2 | (0,1,0,0) |
| 3 | (0,0,1,0) |
| 4 | (0,0,0,1) |
其他4个类型变量的编码方法也是如此,我们可以直接用pandas这一工具完成此操作(首先需要导入包:import pandas as pd)
dummy_fields = ['season', 'weathersit', 'mnth', 'hr', 'weekday'] #所有类型编码变量的名称
for each in dummy_fields:
# 去除所有类型变量,并将它们转变为独热编码
dummies = pd.get_dummies(rides[each], prefix=each, drop_first=False)
# 将新的独热编码变量与原有的所有变量合并到一起
rides = pd.concat([rides, dummies], axis=1)
# 将原来的类型变量从数据表中删除,同时删除后四项分析得到的无关变量
fields_to_drop = ['season', 'weathersit', 'mnth', 'hr', 'weekday', 'instant', 'dteday', 'atemp', 'workingday']
data = rides.drop(fields_to_drop, axis=1)
经过这一番处理,原本只有17列的数据一下子变成了59列,部分如下:
当然可以通过代码查看一下前5行的全部数据:
pd.set_option('display.max_columns', None) #显示所有的列
data.head() #输出前5行全部数据2-2. 数值变量的标准化
剩下的5个自变量只有3个需要处理了,分别为“温度(temp)”、“湿度(hum)”和“风速(windspeed)”,且这3个变量都属于数值变量。因为每个数值变量的变化范围不一样,单位也不一样,因此不同的变量就不能进行比较。我们要把它们都转化到[-1, 1]区间内波动的数值。
比如对于“温度(temp)”这个变量来说,它在'hour.csv'中的平均值为 mean(temp) ,方差为 std(temp) ,那么归一化的温度计算公式为:
$$ temp^{’} = \frac{temp - mean(temp)}{std(temp)} $$
这样处理各数值变量后,它们再输入到网络中可以具有平等的地位:
此处以不对“用户数(cnt)”进行标准化举例。
quant_features = ['temp', 'hum', 'windspeed'] #数值类型变量的名称
scaled_features = {} #将每一个变量的均值和方差都存储到 scaled_features 变量中
for each in quant_features:
# 计算这些变量的均值和方差
mean, std = data[each].mean(), data[each].std()
scaled_features[each] = [mean, std]
# 对每一个变量进行归一化
data.loc[:, each] = (data[each] - mean)/std查看一下数据的前5行:
2-3. 划分数据集
类型变量和数值变量处理结束之后,我们还需要将所有的数据划分为“训练集”和“预测集”两大类,其中,输入到神经网络的只有“训练集”部分,“测试集”相当于是对模型的检验。比如——该数据集是从2011年1月1日开始记录,直到2012年12月31日,每天有24条数据,共17379条记录(去除了缺失值),我们在训练模型时,不让它“看到”后21天的数据,只给它输入前97.1%的数据,让它找这前16875条数据的规律。并且目标值设定为给它“看到”的训练集“用户数(cnt)”值。让模型找到使得训练集损失值最小的各层网络权重和偏置数值,并用此确定的模型来预测“测试集”的因变量“用户数(cnt)”为多少,作图比较,检验对未来的预测效果。
首先划分数据集:
# 对数据进行处理
train_data = data[:-21*24] # 选出训练集
test_data = data[-21*24:] # 选出测试集
# 目标列包含的字段
target_fields = ['cnt', 'casual', 'registered']
# 训练集划分成特征变量列和目标特征列
features, targets = train_data.drop(target_fields, axis=1), train_data[target_fields]
# 测试集划分成特征变量列和目标特征列
test_features, test_targets = test_data.drop(target_fields, axis=1), test_data[target_fields]
# 将数据集类型转换为NumPy数组,float类型
X = features.values #将数据从 pandas dataframe 转换为 NumPy
Y = targets['cnt'].values #要预测的目标是'cnt'
Y = Y.astype(float)
Y = np.reshape(Y, [len(Y), 1])数据划分示意图:
3. 构建神经网络
在数据处理结束后,我们将用PyTorch自带的函数包构建人工神经网络。这个网络有3层:输入层56个神经元、隐含层10个神经元、输出层1个神经元。隐含层的神经元是自定义的,如果设置的太多,容易引起过拟合。
3-1. 自动构建神经网络
使用PyTorch已封装好的函数自动构建我们想要的神经网络如下:
# 定义神经网络架构,features.shape[1]个输入层单元,10个隐含层,1个输出层
input_size = features.shape[1]
hidden_size = 10
output_size = 1
batch_size = 128
neu = torch.nn.Sequential(
torch.nn.Linear(input_size, hidden_size),
torch.nn.Sigmoid(),
torch.nn.Linear(hidden_size, output_size),
) 这些模块包括从输入层到隐含层的线性映射Linear(input_size, hidden_size)、隐含层的非线性 sigmoid函数 torch.nn . Sigmoid(),以及从隐含层到输出层的线性映射torch.nn.Linear(hidden_size, output_size)。
值得注意的是,Sequential里面的层次并不与神经网络的层次严格对应,而是指多步的运算,它与动态计算图的层次相对应。
# 使用PyTorch自带的损失函数
cost = torch.nn.MSELoss()
# 这是PyTorch自带的一个封装好的计算均方误差的损失函数,
# 它是一个函数指针,赋予了变量cost。在计算的时候,
# 我们只需要调用cost(x,y)就可以计算预测向量x和目标向量y之间的均方误差。# 使用PyTorch自带的优化器来自动实现优化算法:
optimizer = torch.optim.SGD(neu.parameters(), lr=0.01)
# torch.optim.SGD()调用了 PyTorch自带的随机梯度下降算法 (stochastic gradient descent,SGD)作为优化器。
# 在初始化optimizer的时候,我们需要待优化的所有参数(在本例中,传入的参数包括神经网络neu包含的所有权重和偏置,
# 即neu. parameters()),以及执行梯度下降算法的学习率lr=0.01。在一切材料都准备好之后,我们便可以实施训练了。
losses = []3-2. 训练数据分批处理
在进行训练循环的时候,我们还会遇到一个问题。在构建的第1个神经网络中,对于每一个训练周期,我们都将所有的数据一次性输入神经网络。这在数据量不大的情况下没有任何问题。但是,现在的数据量是16875条,在这么大数据量的情况下,如果在每个训练周期都处理所有数据,则会出现运算速度过慢、迭代可能不收敛等问题。
解决方法通常是采取批处理(batch processing)的模式,也就是将所有的数据记录划分成一个批次大小 (batch size)的小数据集,然后在每个训练周期给神经网络输入一批数据,如下图所示。批量的大小依问题的复杂度和数据量的大小而定,在本例中,我们设定batch_size=128。
# 神经网络训练循环
for i in range(1000):
# 每128个样本点被划分成一批,在循环的时候一批一批地读取
batch_loss = []
# start 和 end 分别是提取一批数据的起始和终止下标
for start in range(0, len(X), batch_size):
end = start + batch_size if start + batch_size < len(X) else len(X)
xx = Variable(torch.FloatTensor(X[start:end]))
yy = Variable(torch.FloatTensor(Y[start:end]))
predict = neu(xx)
loss = cost(predict, yy)
optimizer.zero_grad()
loss.backward()
optimizer.step()
batch_loss.append(loss.data.numpy())
# 每隔 100 步输出损失值
if i % 100 == 0:
losses.append(np.mean(batch_loss))
print(i, np.mean(batch_loss))
损失值随训练批次的变化:
0 18788.596
100 3003.8276
200 2725.0186
300 2633.2383
400 2591.8367
500 2564.246
600 2527.3044
700 2535.9531
800 2521.357
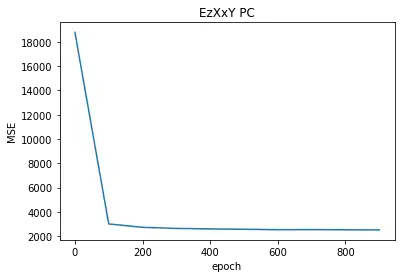
900 2511.4453输出损失值随训练批次的变化曲线:
# 打印输出损失值
plt.plot(np.arange(len(losses)) * 100, losses)
plt.xlabel('epoch')
plt.ylabel('MSE')
plt.title('EzXxY PC')4. 测试神经网络
接下来,我们可以用训练好的神经网络在测试集上进行预测,并且将后21天的预测数据与真实数据画在一起进行比较。
targets = test_targets['cnt'] #读取测试集的cnt数值
targets = targets.values.reshape([len(targets),1]) #将数据转换成合适的tensor形式
targets = targets.astype(float) #保证数据为实数
# 将特征变量和目标变量包裹在Variable型变量中
x = Variable(torch.FloatTensor(test_features.values))
y = Variable(torch.FloatTensor(targets))
# 用神经网络进行预测
predict = neu(x)
predict = predict.data.numpy()
fig, ax = plt.subplots(figsize=(20,8))
ax.plot(predict, label='Prediction')
ax.plot(targets, label='Data')
ax.legend()
ax.set_xlabel('Date-time')
ax.set_ylabel('Counts')
dates = pd.to_datetime(rides.loc[test_data.index]['dteday'])
dates = dates.apply(lambda d: d.strftime('%b %d'))
ax.set_xticks(np.arange(len(dates))[12::24])
_ = ax.set_xticklabels(dates[12::24], rotation=45)
plt.title('EzXxY PC')
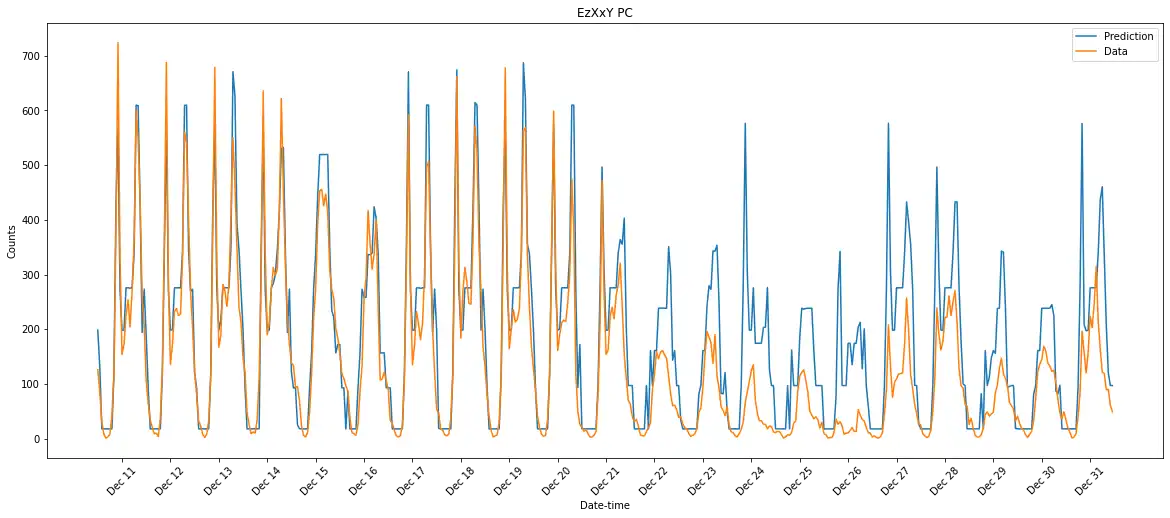
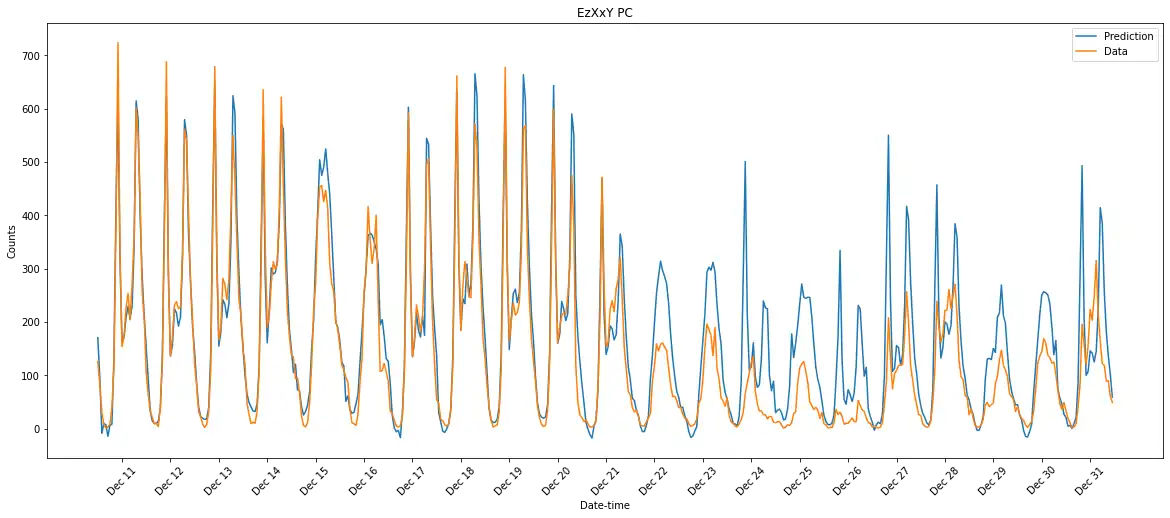
预测结果:
该模型的预测效果与上篇过拟合的结果相比可谓有天壤之别,模型在前11天的各个小时都能够很贴近真实数据,只是在圣诞节前后预测值与真实值的差别较大。这样的模型在非特殊情况下表现结果很是不错,可以用来预测未来。
5. 预测结果对比
本例训练结果与书中将“用户数(cnt)”标准化的结果对比:
5-1. 二者分批次训练的loss值变化数据对比:
本例未标准化的:
0 18788.596
100 3003.8276
200 2725.0186
300 2633.2383
400 2591.8367
500 2564.246
600 2527.3044
700 2535.9531
800 2521.357
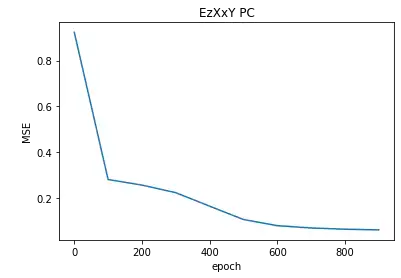
900 2511.4453标准化的:
0 0.9232188
100 0.28176382
200 0.25758424
300 0.22445624
400 0.1658911
500 0.107729204
600 0.0809264
700 0.070677206
800 0.065484814
900 0.062325902这一数值变化并不能说明什么问题,因为计算时本身的范围就不同,我们应当观察曲线的变化趋势。
左侧为本例未标准化的,右侧为标准化了的,从loss值变化趋势来看,不对“用户数(cnt)”进行标准化时,模型收敛地更快一些。
5-2. 预测情况对比
上图为本例未标准化的,下图是标准化了的预测后21天各小时结果图,后者曲线表现得比前者要光滑一些,也更加捕捉到了要预测数据的变化趋势及什么时候该怎么变,而不对“用户数(cnt)”进行标准化的结果中明显表现出有很多该变化的地方是平台般过渡了过去,不太能符合真实数据该有的变化趋势。
综上所述,在相同的计算量前提下,我们可以牺牲一些收敛速度,来追求更加光滑的预测曲线和真实反映数据该有的变化趋势。
6. 小结
数值变量——标准化
torch.nn.MSELoss()——自动损失函数;
torch.optim.SGD()——自动优化器;
batch size——划分为小批次数据
对数值类型的因变量标准化可以使预测曲线更光滑,更加真实地反映出数据的变化趋势。
① 想要了解本例中的PyTorch函数转化为PaddlePaddle函数的方法请点击:→这里
② 想要查看PaddlePaddle实现的本例项目请点击:→这里