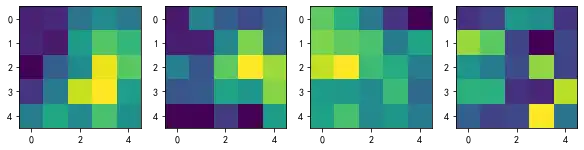了解到卷积神经网络的基本构成和卷积、池化操作原理后，我们只需将池化完成的特征图压扁成一维行向量，就可以作为前馈神经网络的输入数据，进行整体训练了。
让我们对“深度神经网络”中的“Hello World”程序一探究竟吧！
①介绍：卷积神经网络(CNN)可以自动提取非结构化数据的特征，对本例而言，它可以自动学习手写数字图像的本质特征。
②前提：对卷和池化操作的理解，前馈神经网络的搭建，分类模型的实现。
模型概况
① 数据集为28×28的手写数字图像；
② 网络架构分为特征提取层和用于分类的前馈神经网络；
③ 特征提取层分为四层：平面卷积层得到4×28×28的特征图，池化层得到4×14×14的轮廓特征图，立体卷积层得到8×14×14的特征图，池化层得到8×7×7的轮廓特征图；
④ 用于分类的前馈网络将8×7×7=392的轮廓特征图排列为大小为392的行向量，经过512个神经元的隐含层，得到0~9这10个数字的概率值。
② 网络架构分为特征提取层和用于分类的前馈神经网络；
③ 特征提取层分为四层：平面卷积层得到4×28×28的特征图，池化层得到4×14×14的轮廓特征图，立体卷积层得到8×14×14的特征图，池化层得到8×7×7的轮廓特征图；
④ 用于分类的前馈网络将8×7×7=392的轮廓特征图排列为大小为392的行向量，经过512个神经元的隐含层，得到0~9这10个数字的概率值。
1. 期望目标：
① 如何使用
PyTorch自带的数据集、数据加载器和采样器
② 如何实现防止过拟合的
dropout技术及其原理
③ 观察各层提取出的特征图的样子
2. 使用PyTorch自带的数据集、数据加载器和采样器加载并处理数据
# 导入所有需要用到的包
import torch
import torch.nn as nn
from torch.autograd import Variable
import torch.optim as optim
import torch.nn.functional as F
import torchvision.datasets as dsets
import torchvision.transforms as transforms
import matplotlib.pyplot as plt
import numpy as np
#以下语句可以让Jupyter Notebook直接输出图像%matplotlib inline
%matplotlib inline# 定义训练超参数
image_size = 28 #图像总尺寸为28×28
num_classes =10 #标签的种类数
num_epochs = 20 #训练的总循环周期
batch_size = 64 #—个批次的大小，64张图片用PyTorch自带的方法，自动下载MNIST数据集到本地当前目录的'./数据集/3.MNIST'文件夹下，并使用加载器加载到内存中。
# 加载MNIST数据，自动下载到当前目录下的'数据集/3.MNIST'子目录
# MNIST 数据属于 torchvision 包自带的数据，可以直接调用
# 当用户想调用自己的图像数据时，可以用 torchvision.datasets.ImageFolder 或 torch.utils.data.TensorDataset 来加载
train_dataset = dsets.MNIST(root='./数据集/3.MNIST', #文件存放路径
train=True, #提取训练集
#将图像转化为 Tensor ,在加载数据时,就可以对图像做预处理
transform=transforms.ToTensor(),
download=True) #当找不到文件的时候,自动下载
# 加载测试数据集
test_dataset = dsets.MNIST(root='./数据集/3.MNIST',
train=False,
transform=transforms.ToTensor())
# 训练数据集的加载器，自动将数据切分成批，顺序随机打乱
train_loader = torch.utils.data.DataLoader(dataset=train_dataset,
batch_size=batch_size,
shuffle=True)
# 我们希望将测试数据分成两部分，一部分作为校验数据，一部分作为测试数据。校验数据用于检测模型是否过拟合并调整参数，测试数据检验整个模型的工作
# 首先，定义下标数组 indices ，它相当于对所有 test_dataset 中数据的编码
# 然后，定义下标 indices_val 表示校验集数据的下标，indices_test 表示测试集的下标
indices = range(len(test_dataset))
indices_val = indices[:5000]
indices_test = indices[5000:]
# 根据下标构造两个数据集的 SubsetRandomSampler 采样器，它会对下标进行采样
sampler_val = torch.utils.data.sampler.SubsetRandomSampler(indices_val)
sampler_test = torch.utils.data.sampler.SubsetRandomSampler(indices_test)
# 根据两个采样器定义加载器
# 注意将 sampler_val 和 sampler_test 分别赋值给了 validation_loader 和 test_loader
validation_loader = torch.utils.data.DataLoader(dataset=test_dataset,
batch_size=batch_size,
shuffle=False,
sampler=sampler_val)
test_loader = torch.utils.data.DataLoader(dataset=test_dataset,
batch_size=batch_size,
shuffle=False,
sampler=sampler_test)
对于已经处理好的数据，我们可以直接根据索引去提取，并通过Python的绘图处理包将手写数字显示出来
# 随便从数据集中读入一张图片，并绘制出来
idx = 100
# dataset 支持下标索引，其中提取出来的元素为 features、target 格式、即属性和标签
muteimg = train_dataset[idx][0].numpy()
# 一般的图像包含 RGB 这3个通道，而 MNIST 数据集的图像都是灰度的,只有一个通道
# 因此，我们忽略通道，把图像看作一个灰度矩阵
# 用 imshow 画图，会将灰度矩阵自动展现为彩色，不同灰度对应不同的颜色：从黄到紫
plt.imshow(muteimg[0,...])
print('标签是：',train_dataset[idx][1])
标签是： 5
3. 使用nn.Module类来构建经典的卷积神经网络
# 定义卷积神经网络：4 和 8 为人为指定的两个卷积层的厚度（feature map 的数量）
depth = [4, 8]
class ConvNet(nn.Module):
def __init__(self):
# 该函数在创建一个 ConvNet 对象即调用语句 net=ConvNet() 时就会被调用
# 首先调用父类相应的构造函数
super(ConvNet, self).__init__()
# 其次构造 ConvNet 需要用到的各个神经模块
# 注意，定义组件并不是真正搭建组件，只是把基本建筑砖块先找好
# 定义一个卷积层，输入通道为 1（灰度图），输出通道为 4（第一个卷积核个数），窗口大小为 5（卷积核大小为5×5），padding为 2（原始图像外面补2圈0）
self.conv1 = nn.Conv2d(1, 4, 5, padding=2)
self.pool = nn.MaxPool2d(2, 2) #定义一个池化层，一个窗口为2x2的池化运算
# 第二层卷积，输入通道为 depth[0]，输出通道为 depth[1]，窗口为 5，padding 为 2
self.conv2 = nn.Conv2d(depth[0], depth[1], 5, padding=2)
# 一个线性连接层，输入尺寸为最后一层立方体的线性平铺，输出层 512 个节点
self.fc1 = nn.Linear(image_size // 4 * image_size // 4 * depth[1], 512)
self.fc2 = nn.Linear(512, num_classes) #最后一层线性分类单元，输入为 512，输出为要做分类的类别数
# 定义完成神经网络真正的前向运算，在这里把各个组件进行实际的拼装
def forward(self, x):
# 目前x的尺寸：(batch_size, image_channels, image_width, image_height)
x = self.conv1(x) #第一层卷积
x = F.relu(x) #激活函数用ReLU，防止过拟合
# 目前x的尺寸：(batch_size, num_filters, image_width, image_height)
x = self.pool(x) #第二层池化，将图片缩小
# 目前x的尺寸：(batch_size, depth[0], image_width/2, image_height/2)
x = self.conv2(x) #第三层又是卷积，窗口为 5，输入输出通道分别为 depth[0]=4, depth[1]=8
x = F.relu(x) #非线性函数
# 目前x的尺寸:(batch_size, depth[1], image_width/2，image_height/2)
x = self.pool(x)#第四层池化，将图片缩小到原来的1/4
# 目前x的尺寸：(batch_size, depth[1], image_width/4, image_height/4)
# 将立体的特征图 tensor 压成一个一维的向量
# view 函数可以将一个 tensor 按指定的方式重新排布
# 下面这个命令就是要让x按照 batch_size * (image_size//4)^2 * depth[1] 的方式来排布向量
x = x.view(-1, image_size // 4 * image_size // 4 * depth[1])
# 目前x的尺寸：(batch_size, depth[1]*image_width/4*image_height/4)
x = F.relu(self.fc1(x)) #第五层为全连接，ReLU激活函数
# 目前x的尺寸：(batch_size, 512)
# 以默认0.5的概率对这一层进行 dropout 操作，防止过拟合
x = F.dropout(x, training=self.training)
x = self.fc2(x) #全连接
# 目前x的尺寸：(batch_size, num_classes)
# 输出层为 log_softmax，即概率对数值 log(p(x))，采用 log_softmax 可以使后面的交叉熵计算更快
x = F.log_softmax(x, dim=1)
return x
def retrieve_features(self, x):
# 该函数用于提取卷积神经网络的特征图，返回 feature_map1， feature_map2 为前两层卷积层的特征图
feature_map1 = F.relu(self.conv1(x)) #完成第一层卷积
x = self.pool(feature_map1) #完成第一层池化
# 第二层卷积，两层特征图都存储到了 feature_map1, feature_map2 中
feature_map2 = F.relu(self.conv2(x))
return (feature_map1, feature_map2)
# 自定义的计算一组数据分类准确度的函数
# prediction 为模型给出的预测结果，labels 为数据中的标签，比较二者以确定整个神经网络当前的表现
def rightness(predictions, labels):
# 计算预测错误率的函数、其中 predictions 是模型给出的一组预测结果，batch size行num classes列的
# 矩阵,labels是数据中的正确答案
# 对于任意一行(一个样本)的输出值的第1个维度求最大，得到每一行最大元素的下标
pred = torch.max(predictions.data, 1)[1]
# 将下标与labels中包含的类别进行比较,并累计得到比较正确的数量
rights = pred.eq(labels.data.view_as(pred)).sum()
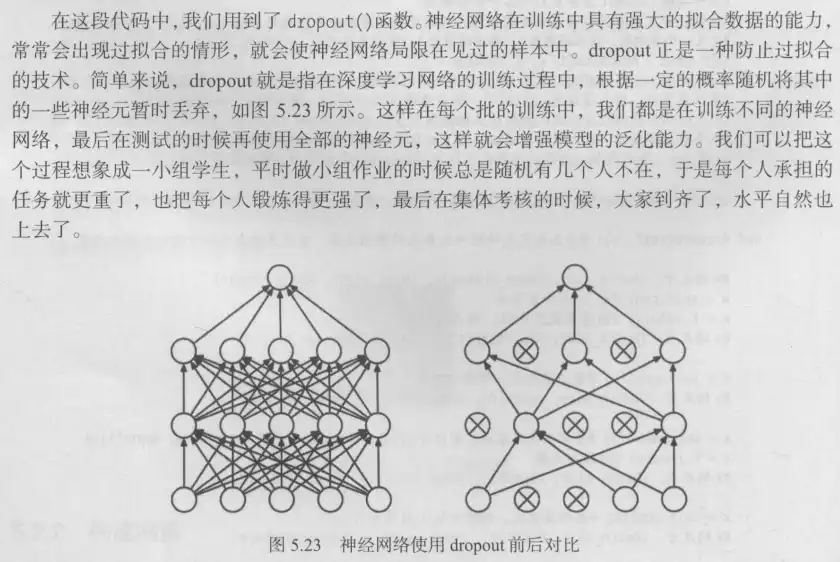
return rights, len(labels) #返回正确的数量和这一次一共比较了多少元素在这段代码中用到了dropout()函数，它是一种防止过拟合的技术。在深度学习网络的训练过程中，根据一定的概率随机将其中的一些神经元暂时丢弃，如下图所示。这样在每个批的训练中，我们都是在训练不同的神经网络，最后在测试的时候再使用全部的神经元，这样做可以增强模型的泛化能力。这个过程可以理解为：一组学生在平时做总任务量不变的小组作业时，总是随机有几个人不在场，于是每个人承担的任务就更重了，也把每个人锻炼地更强了，最后在集体考核的时候，大家到齐了，水平自然会提高。
4. 训练网络模型
构建好我们的 ConvNet 之后，就可以读取数据并开始训练了。
# 新建一个卷积神经网络的实例，此时 ConvNet 的__init__()函数会被自动调用
net = ConvNet()
criterion = nn.CrossEntropyLoss() #Loss函数的定义，交叉熵
optimizer = optim.SGD(net.parameters(), lr=0.001, momentum=0.9) #定义优化器，普通的随机梯度下降算法
record = [] #记录准确率等数值的容器
weights = [] #每若干次就提交一次卷积核
# 开始训练循环
for epoch in range(num_epochs):
train_rights = [] #记录训练数据集准确率的容器
''' 下面的 enumerate 起到构造一个枚举器的作用。在对train loader做循环迭代时，
enumerate 会自动输出一个数字指示循环了几次，并记录在batch_idx中，
它就等于0,1,2，...train_loader每迭代一次，就会输出一对数据data和target，
分别对应一个批中的手写数字图及对应的标签。 '''
# 针对容器中的每一个批进行循环
for batch_idx, (data, target) in enumerate(train_loader):
# 将 Tensor 转化为 Variable, data 为一批图像，target 为一批标签
data, target = Variable(data), Variable(target)
# 给网络模型做标记，标志着模型在训练集上训练
# 这种区分主要是为了打开关闭 net 的 training 标志，从而决定是否运行 dropout
net.train()
output = net(data) #神经网络完成一次前馈的计算过程，得到预测输出 output
loss = criterion(output, target) #将 output 与标签 target 比较，计算误差
optimizer.zero_grad() #清空梯度
loss.backward() #反向传播
optimizer.step() #一步随机梯度下降算法
right = rightness(output, target) #计算准确率所需数值，返回数值为（正确样例数，总样本数）
train_rights.append(right) #将计算结果装到列表容器 train_rights 中
# 每间隔100个batch执行一次打印操作
if batch_idx % 100 == 0:
net.eval() #给网络模型做标记，标志着模型在训练集上训练
val_rights = [] #记录校验数据及准确率的容器
# 开始在校验集上做循环，计算校验集上的准确度
for (data, target) in validation_loader:
data, target = Variable(data), Variable(target)
# 完成一次前馈计算过程，得到目前训练得到的模型 net 在校验集上的表现
output = net(data)
# 计算准确率所需数值，返回正确的数值为（正确样例数，总样本数）
right = rightness(output, target)
val_rights.append(right)
# 分别计算目前已经计算过的测试集以及全部校验集上模型的表现：分类准确率
# train_r 为一个二元组，分别记录经历过的所有训练集中分类正确的数量和该集合中总的样本数
# train_r[0]/train_r[1] 是训练集的分类准确度，val_r[0]/val_r[1]是校验集的分类准确度
train_r = (sum([tup[0] for tup in train_rights]), sum([tup[1] for tup in train_rights]))
# val_r 为一个二元组，分别记录校验集中分类正确的数量和该集合中总的样本数
val_r = (sum([tup[0] for tup in val_rights]), sum([tup[1] for tup in val_rights]))
# 打印准确率等数值，其中正确率为本训练周期 epoch 开始后到目前批的正确率平均值
print('训练周期：{} [{}/{}({:.0f}%)]\t，loss：{:.4f}\t，训练正确率：{:.2f}%\t，校验正确率：{}%'.format(
epoch, batch_idx * len(data), len(train_loader.dataset),
100. * batch_idx / len(train_loader), loss.item(),
100. * train_r[0] / train_r[1],
100. * val_r[0] / val_r[1]))
# 将准确率和权重等数值加载到容器中，方便后续处理
record.append((100 - 100. * train_r[0] / train_r[1], 100 - 100. * val_r[0] / val_r[1]))
# weights 记录了训练周期中所有卷积核的演化过程，net.conv1.weight 提取出了第一层卷积核的权重
# clone 是将 weight.data 中的数据做一个备份放到列表中
# 否则当 weight.data 变化时，列表中的每一项数值也会联动
# 这里使用 clone 这个函数很重要
weights.append([net.conv1.weight.data.clone(), net.conv1.bias.data.clone(),
net.conv2.weight.data.clone(), net.conv2.bias.data.clone()])
训练周期：0 [0/60000(0%)] ，loss：2.3029 ，训练正确率：7.81% ，校验正确率：13.140000343322754%
训练周期：0 [800/60000(11%)] ，loss：2.2597 ，训练正确率：18.66% ，校验正确率：31.739999771118164%
训练周期：0 [1600/60000(21%)] ，loss：2.1839 ，训练正确率：24.80% ，校验正确率：39.939998626708984%
训练周期：0 [2400/60000(32%)] ，loss：1.7840 ，训练正确率：31.10% ，校验正确率：58.34000015258789%
训练周期：0 [3200/60000(43%)] ，loss：0.7455 ，训练正确率：38.38% ，校验正确率：74.86000061035156%
训练周期：0 [4000/60000(53%)] ，loss：0.8256 ，训练正确率：45.42% ，校验正确率：79.62000274658203%
训练周期：0 [4800/60000(64%)] ，loss：0.7085 ，训练正确率：51.09% ，校验正确率：81.13999938964844%
训练周期：0 [5600/60000(75%)] ，loss：0.6540 ，训练正确率：55.59% ，校验正确率：84.72000122070312%
训练周期：0 [6400/60000(85%)] ，loss：0.5010 ，训练正确率：59.19% ，校验正确率：86.94000244140625%
训练周期：0 [7200/60000(96%)] ，loss：0.3282 ，训练正确率：62.09% ，校验正确率：87.44000244140625%
训练周期：1 [0/60000(0%)] ，loss：0.4386 ，训练正确率：85.94% ，校验正确率：87.13999938964844%
训练周期：1 [800/60000(11%)] ，loss：0.2445 ，训练正确率：87.38% ，校验正确率：87.86000061035156%
训练周期：1 [1600/60000(21%)] ，loss：0.1772 ，训练正确率：87.97% ，校验正确率：88.95999908447266%
训练周期：1 [2400/60000(32%)] ，loss：0.2384 ，训练正确率：88.24% ，校验正确率：88.94000244140625%
训练周期：1 [3200/60000(43%)] ，loss：0.2126 ，训练正确率：88.51% ，校验正确率：90.04000091552734%
训练周期：1 [4000/60000(53%)] ，loss：0.3798 ，训练正确率：88.74% ，校验正确率：90.87999725341797%
训练周期：1 [4800/60000(64%)] ，loss：0.2175 ，训练正确率：88.93% ，校验正确率：91.0999984741211%
训练周期：1 [5600/60000(75%)] ，loss：0.4422 ，训练正确率：89.12% ，校验正确率：91.5199966430664%
训练周期：1 [6400/60000(85%)] ，loss：0.1111 ，训练正确率：89.33% ，校验正确率：91.5999984741211%
训练周期：1 [7200/60000(96%)] ，loss：0.1762 ，训练正确率：89.56% ，校验正确率：92.0199966430664%
训练周期：2 [0/60000(0%)] ，loss：0.1034 ，训练正确率：98.44% ，校验正确率：92.13999938964844%
训练周期：2 [800/60000(11%)] ，loss：0.0949 ，训练正确率：91.88% ，校验正确率：91.80000305175781%
训练周期：2 [1600/60000(21%)] ，loss：0.1513 ，训练正确率：92.13% ，校验正确率：92.5199966430664%
训练周期：2 [2400/60000(32%)] ，loss：0.2159 ，训练正确率：92.01% ，校验正确率：92.95999908447266%
训练周期：2 [3200/60000(43%)] ，loss：0.1311 ，训练正确率：92.13% ，校验正确率：93.0199966430664%
训练周期：2 [4000/60000(53%)] ，loss：0.1233 ，训练正确率：92.18% ，校验正确率：93.37999725341797%
训练周期：2 [4800/60000(64%)] ，loss：0.2501 ，训练正确率：92.25% ，校验正确率：92.91999816894531%
训练周期：2 [5600/60000(75%)] ，loss：0.0885 ，训练正确率：92.35% ，校验正确率：93.5%
训练周期：2 [6400/60000(85%)] ，loss：0.2350 ，训练正确率：92.40% ，校验正确率：93.87999725341797%
训练周期：2 [7200/60000(96%)] ，loss：0.2525 ，训练正确率：92.50% ，校验正确率：93.45999908447266%
训练周期：3 [0/60000(0%)] ，loss：0.2652 ，训练正确率：92.19% ，校验正确率：93.4000015258789%
训练周期：3 [800/60000(11%)] ，loss：0.2486 ，训练正确率：93.72% ，校验正确率：93.77999877929688%
训练周期：3 [1600/60000(21%)] ，loss：0.1579 ，训练正确率：93.75% ，校验正确率：94.0%
训练周期：3 [2400/60000(32%)] ，loss：0.1064 ，训练正确率：93.74% ，校验正确率：94.12000274658203%
训练周期：3 [3200/60000(43%)] ，loss：0.1737 ，训练正确率：93.89% ，校验正确率：94.4800033569336%
训练周期：3 [4000/60000(53%)] ，loss：0.3349 ，训练正确率：93.88% ，校验正确率：94.5%
训练周期：3 [4800/60000(64%)] ，loss：0.1476 ，训练正确率：93.91% ，校验正确率：94.18000030517578%
训练周期：3 [5600/60000(75%)] ，loss：0.1594 ，训练正确率：93.94% ，校验正确率：94.66000366210938%
训练周期：3 [6400/60000(85%)] ，loss：0.3077 ，训练正确率：93.98% ，校验正确率：94.41999816894531%
训练周期：3 [7200/60000(96%)] ，loss：0.0843 ，训练正确率：94.03% ，校验正确率：94.72000122070312%
训练周期：4 [0/60000(0%)] ，loss：0.2381 ，训练正确率：92.19% ，校验正确率：94.9000015258789%
训练周期：4 [800/60000(11%)] ，loss：0.1409 ，训练正确率：94.21% ，校验正确率：94.73999786376953%
训练周期：4 [1600/60000(21%)] ，loss：0.4307 ，训练正确率：94.51% ，校验正确率：94.77999877929688%
训练周期：4 [2400/60000(32%)] ，loss：0.1203 ，训练正确率：94.62% ，校验正确率：95.23999786376953%
训练周期：4 [3200/60000(43%)] ，loss：0.4092 ，训练正确率：94.74% ，校验正确率：95.36000061035156%
训练周期：4 [4000/60000(53%)] ，loss：0.1616 ，训练正确率：94.73% ，校验正确率：94.76000213623047%
训练周期：4 [4800/60000(64%)] ，loss：0.1276 ，训练正确率：94.81% ，校验正确率：94.76000213623047%
训练周期：4 [5600/60000(75%)] ，loss：0.3130 ，训练正确率：94.83% ，校验正确率：95.04000091552734%
训练周期：4 [6400/60000(85%)] ，loss：0.1837 ，训练正确率：94.89% ，校验正确率：95.33999633789062%
训练周期：4 [7200/60000(96%)] ，loss：0.0961 ，训练正确率：94.88% ，校验正确率：95.45999908447266%
训练周期：5 [0/60000(0%)] ，loss：0.1527 ，训练正确率：96.88% ，校验正确率：95.63999938964844%
训练周期：5 [800/60000(11%)] ，loss：0.3296 ，训练正确率：95.34% ，校验正确率：95.23999786376953%
训练周期：5 [1600/60000(21%)] ，loss：0.1865 ，训练正确率：95.25% ，校验正确率：95.80000305175781%
训练周期：5 [2400/60000(32%)] ，loss：0.1548 ，训练正确率：95.15% ，校验正确率：95.55999755859375%
训练周期：5 [3200/60000(43%)] ，loss：0.2680 ，训练正确率：95.11% ，校验正确率：95.73999786376953%
训练周期：5 [4000/60000(53%)] ，loss：0.1539 ，训练正确率：95.15% ，校验正确率：95.80000305175781%
训练周期：5 [4800/60000(64%)] ，loss：0.2378 ，训练正确率：95.21% ，校验正确率：95.81999969482422%
训练周期：5 [5600/60000(75%)] ，loss：0.1700 ，训练正确率：95.17% ，校验正确率：95.80000305175781%
训练周期：5 [6400/60000(85%)] ，loss：0.1820 ，训练正确率：95.23% ，校验正确率：95.95999908447266%
训练周期：5 [7200/60000(96%)] ，loss：0.0674 ，训练正确率：95.27% ，校验正确率：96.04000091552734%
训练周期：6 [0/60000(0%)] ，loss：0.1380 ，训练正确率：93.75% ，校验正确率：96.16000366210938%
训练周期：6 [800/60000(11%)] ，loss：0.1632 ，训练正确率：95.78% ，校验正确率：96.05999755859375%
训练周期：6 [1600/60000(21%)] ，loss：0.2500 ，训练正确率：95.70% ，校验正确率：96.0199966430664%
训练周期：6 [2400/60000(32%)] ，loss：0.3072 ，训练正确率：95.62% ，校验正确率：95.95999908447266%
训练周期：6 [3200/60000(43%)] ，loss：0.2378 ，训练正确率：95.72% ，校验正确率：96.08000183105469%
训练周期：6 [4000/60000(53%)] ，loss：0.1097 ，训练正确率：95.64% ，校验正确率：95.83999633789062%
训练周期：6 [4800/60000(64%)] ，loss：0.0986 ，训练正确率：95.65% ，校验正确率：96.18000030517578%
训练周期：6 [5600/60000(75%)] ，loss：0.1341 ，训练正确率：95.71% ，校验正确率：96.23999786376953%
训练周期：6 [6400/60000(85%)] ，loss：0.0736 ，训练正确率：95.71% ，校验正确率：96.22000122070312%
训练周期：6 [7200/60000(96%)] ，loss：0.1628 ，训练正确率：95.77% ，校验正确率：96.36000061035156%
训练周期：7 [0/60000(0%)] ，loss：0.1379 ，训练正确率：90.62% ，校验正确率：96.4800033569336%
训练周期：7 [800/60000(11%)] ，loss：0.2877 ，训练正确率：96.02% ，校验正确率：96.41999816894531%
训练周期：7 [1600/60000(21%)] ，loss：0.0860 ，训练正确率：96.20% ，校验正确率：96.26000213623047%
训练周期：7 [2400/60000(32%)] ，loss：0.1080 ，训练正确率：96.23% ，校验正确率：96.54000091552734%
训练周期：7 [3200/60000(43%)] ，loss：0.1141 ，训练正确率：96.22% ，校验正确率：96.54000091552734%
训练周期：7 [4000/60000(53%)] ，loss：0.1179 ，训练正确率：96.27% ，校验正确率：96.31999969482422%
训练周期：7 [4800/60000(64%)] ，loss：0.1088 ，训练正确率：96.23% ，校验正确率：96.37999725341797%
训练周期：7 [5600/60000(75%)] ，loss：0.0963 ，训练正确率：96.22% ，校验正确率：96.33999633789062%
训练周期：7 [6400/60000(85%)] ，loss：0.2227 ，训练正确率：96.19% ，校验正确率：96.58000183105469%
训练周期：7 [7200/60000(96%)] ，loss：0.2242 ，训练正确率：96.22% ，校验正确率：96.68000030517578%
训练周期：8 [0/60000(0%)] ，loss：0.0941 ，训练正确率：95.31% ，校验正确率：95.83999633789062%
训练周期：8 [800/60000(11%)] ，loss：0.0596 ，训练正确率：96.02% ，校验正确率：96.68000030517578%
训练周期：8 [1600/60000(21%)] ，loss：0.0772 ，训练正确率：96.17% ，校验正确率：96.5999984741211%
训练周期：8 [2400/60000(32%)] ，loss：0.2326 ，训练正确率：96.27% ，校验正确率：96.9000015258789%
训练周期：8 [3200/60000(43%)] ，loss：0.0502 ，训练正确率：96.43% ，校验正确率：96.77999877929688%
训练周期：8 [4000/60000(53%)] ，loss：0.0481 ，训练正确率：96.48% ，校验正确率：96.83999633789062%
训练周期：8 [4800/60000(64%)] ，loss：0.0423 ，训练正确率：96.55% ，校验正确率：96.72000122070312%
训练周期：8 [5600/60000(75%)] ，loss：0.1444 ，训练正确率：96.61% ，校验正确率：96.81999969482422%
训练周期：8 [6400/60000(85%)] ，loss：0.0863 ，训练正确率：96.61% ，校验正确率：96.68000030517578%
训练周期：8 [7200/60000(96%)] ，loss：0.0692 ，训练正确率：96.59% ，校验正确率：96.4000015258789%
训练周期：9 [0/60000(0%)] ，loss：0.0957 ，训练正确率：96.88% ，校验正确率：96.5999984741211%
训练周期：9 [800/60000(11%)] ，loss：0.1353 ，训练正确率：96.41% ，校验正确率：96.80000305175781%
训练周期：9 [1600/60000(21%)] ，loss：0.1883 ，训练正确率：96.44% ，校验正确率：96.86000061035156%
训练周期：9 [2400/60000(32%)] ，loss：0.0810 ，训练正确率：96.52% ，校验正确率：96.72000122070312%
训练周期：9 [3200/60000(43%)] ，loss：0.3609 ，训练正确率：96.60% ，校验正确率：96.91999816894531%
训练周期：9 [4000/60000(53%)] ，loss：0.0661 ，训练正确率：96.55% ，校验正确率：96.9000015258789%
训练周期：9 [4800/60000(64%)] ，loss：0.0842 ，训练正确率：96.55% ，校验正确率：96.72000122070312%
训练周期：9 [5600/60000(75%)] ，loss：0.0735 ，训练正确率：96.63% ，校验正确率：97.0%
训练周期：9 [6400/60000(85%)] ，loss：0.1281 ，训练正确率：96.66% ，校验正确率：97.0199966430664%
训练周期：9 [7200/60000(96%)] ，loss：0.0413 ，训练正确率：96.67% ，校验正确率：97.04000091552734%
训练周期：10 [0/60000(0%)] ，loss：0.1483 ，训练正确率：96.88% ，校验正确率：97.08000183105469%
训练周期：10 [800/60000(11%)] ，loss：0.1941 ，训练正确率：97.01% ，校验正确率：97.05999755859375%
训练周期：10 [1600/60000(21%)] ，loss：0.0622 ，训练正确率：97.13% ，校验正确率：96.73999786376953%
训练周期：10 [2400/60000(32%)] ，loss：0.1103 ，训练正确率：97.08% ，校验正确率：96.9800033569336%
训练周期：10 [3200/60000(43%)] ，loss：0.2204 ，训练正确率：97.05% ，校验正确率：96.72000122070312%
训练周期：10 [4000/60000(53%)] ，loss：0.1628 ，训练正确率：97.00% ，校验正确率：96.9000015258789%
训练周期：10 [4800/60000(64%)] ，loss：0.0427 ，训练正确率：97.00% ，校验正确率：96.91999816894531%
训练周期：10 [5600/60000(75%)] ，loss：0.0624 ，训练正确率：96.99% ，校验正确率：97.12000274658203%
训练周期：10 [6400/60000(85%)] ，loss：0.0405 ，训练正确率：96.96% ，校验正确率：97.19999694824219%
训练周期：10 [7200/60000(96%)] ，loss：0.1101 ，训练正确率：96.94% ，校验正确率：96.9800033569336%
训练周期：11 [0/60000(0%)] ，loss：0.4243 ，训练正确率：92.19% ，校验正确率：97.31999969482422%
训练周期：11 [800/60000(11%)] ，loss：0.0814 ，训练正确率：96.84% ，校验正确率：97.26000213623047%
训练周期：11 [1600/60000(21%)] ，loss：0.0442 ，训练正确率：97.00% ，校验正确率：97.04000091552734%
训练周期：11 [2400/60000(32%)] ，loss：0.1228 ，训练正确率：97.04% ，校验正确率：96.9800033569336%
训练周期：11 [3200/60000(43%)] ，loss：0.0914 ，训练正确率：97.03% ，校验正确率：97.27999877929688%
训练周期：11 [4000/60000(53%)] ，loss：0.1118 ，训练正确率：97.02% ，校验正确率：97.0199966430664%
训练周期：11 [4800/60000(64%)] ，loss：0.1928 ，训练正确率：97.10% ，校验正确率：97.04000091552734%
训练周期：11 [5600/60000(75%)] ，loss：0.2477 ，训练正确率：97.10% ，校验正确率：97.0999984741211%
训练周期：11 [6400/60000(85%)] ，loss：0.2033 ，训练正确率：97.09% ，校验正确率：96.86000061035156%
训练周期：11 [7200/60000(96%)] ，loss：0.0779 ，训练正确率：97.08% ，校验正确率：97.0199966430664%
训练周期：12 [0/60000(0%)] ，loss：0.0612 ，训练正确率：96.88% ，校验正确率：97.0999984741211%
训练周期：12 [800/60000(11%)] ，loss：0.1056 ，训练正确率：97.14% ，校验正确率：97.05999755859375%
训练周期：12 [1600/60000(21%)] ，loss：0.0705 ，训练正确率：97.17% ，校验正确率：97.04000091552734%
训练周期：12 [2400/60000(32%)] ，loss：0.0337 ，训练正确率：97.27% ，校验正确率：97.0999984741211%
训练周期：12 [3200/60000(43%)] ，loss：0.1298 ，训练正确率：97.24% ，校验正确率：97.4000015258789%
训练周期：12 [4000/60000(53%)] ，loss：0.1841 ，训练正确率：97.21% ，校验正确率：97.22000122070312%
训练周期：12 [4800/60000(64%)] ，loss：0.0627 ，训练正确率：97.26% ，校验正确率：97.33999633789062%
训练周期：12 [5600/60000(75%)] ，loss：0.0234 ，训练正确率：97.30% ，校验正确率：97.41999816894531%
训练周期：12 [6400/60000(85%)] ，loss：0.1213 ，训练正确率：97.23% ，校验正确率：97.4000015258789%
训练周期：12 [7200/60000(96%)] ，loss：0.0512 ，训练正确率：97.23% ，校验正确率：97.33999633789062%
训练周期：13 [0/60000(0%)] ，loss：0.0209 ，训练正确率：100.00% ，校验正确率：97.44000244140625%
训练周期：13 [800/60000(11%)] ，loss：0.0335 ，训练正确率：97.56% ，校验正确率：97.30000305175781%
训练周期：13 [1600/60000(21%)] ，loss：0.0689 ，训练正确率：97.43% ，校验正确率：97.23999786376953%
训练周期：13 [2400/60000(32%)] ，loss：0.0116 ，训练正确率：97.40% ，校验正确率：97.23999786376953%
训练周期：13 [3200/60000(43%)] ，loss：0.1370 ，训练正确率：97.36% ，校验正确率：97.37999725341797%
训练周期：13 [4000/60000(53%)] ，loss：0.0666 ，训练正确率：97.45% ，校验正确率：97.5199966430664%
训练周期：13 [4800/60000(64%)] ，loss：0.0250 ，训练正确率：97.33% ，校验正确率：97.62000274658203%
训练周期：13 [5600/60000(75%)] ，loss：0.0766 ，训练正确率：97.40% ，校验正确率：97.5199966430664%
训练周期：13 [6400/60000(85%)] ，loss：0.0687 ，训练正确率：97.38% ，校验正确率：97.22000122070312%
训练周期：13 [7200/60000(96%)] ，loss：0.2075 ，训练正确率：97.37% ，校验正确率：97.5%
训练周期：14 [0/60000(0%)] ，loss：0.0757 ，训练正确率：96.88% ，校验正确率：97.33999633789062%
训练周期：14 [800/60000(11%)] ，loss：0.0381 ，训练正确率：97.63% ，校验正确率：97.08000183105469%
训练周期：14 [1600/60000(21%)] ，loss：0.0535 ，训练正确率：97.53% ，校验正确率：97.41999816894531%
训练周期：14 [2400/60000(32%)] ，loss：0.1192 ，训练正确率：97.56% ，校验正确率：97.5%
训练周期：14 [3200/60000(43%)] ，loss：0.0566 ，训练正确率：97.49% ，校验正确率：97.33999633789062%
训练周期：14 [4000/60000(53%)] ，loss：0.0209 ，训练正确率：97.48% ，校验正确率：97.45999908447266%
训练周期：14 [4800/60000(64%)] ，loss：0.0291 ，训练正确率：97.55% ，校验正确率：97.58000183105469%
训练周期：14 [5600/60000(75%)] ，loss：0.1973 ，训练正确率：97.59% ，校验正确率：97.5999984741211%
训练周期：14 [6400/60000(85%)] ，loss：0.1711 ，训练正确率：97.58% ，校验正确率：97.55999755859375%
训练周期：14 [7200/60000(96%)] ，loss：0.0081 ，训练正确率：97.55% ，校验正确率：97.5199966430664%
训练周期：15 [0/60000(0%)] ，loss：0.0778 ，训练正确率：96.88% ，校验正确率：97.44000244140625%
训练周期：15 [800/60000(11%)] ，loss：0.2654 ，训练正确率：97.48% ，校验正确率：97.33999633789062%
训练周期：15 [1600/60000(21%)] ，loss：0.0384 ，训练正确率：97.61% ，校验正确率：97.45999908447266%
训练周期：15 [2400/60000(32%)] ，loss：0.0111 ，训练正确率：97.64% ，校验正确率：97.41999816894531%
训练周期：15 [3200/60000(43%)] ，loss：0.0667 ，训练正确率：97.62% ，校验正确率：97.5999984741211%
训练周期：15 [4000/60000(53%)] ，loss：0.2147 ，训练正确率：97.57% ，校验正确率：97.45999908447266%
训练周期：15 [4800/60000(64%)] ，loss：0.0654 ，训练正确率：97.55% ，校验正确率：97.33999633789062%
训练周期：15 [5600/60000(75%)] ，loss：0.1121 ，训练正确率：97.54% ，校验正确率：97.5999984741211%
训练周期：15 [6400/60000(85%)] ，loss：0.0139 ，训练正确率：97.55% ，校验正确率：97.55999755859375%
训练周期：15 [7200/60000(96%)] ，loss：0.0254 ，训练正确率：97.57% ，校验正确率：97.55999755859375%
训练周期：16 [0/60000(0%)] ，loss：0.0343 ，训练正确率：98.44% ，校验正确率：97.4000015258789%
训练周期：16 [800/60000(11%)] ，loss：0.0742 ，训练正确率：97.87% ，校验正确率：97.58000183105469%
训练周期：16 [1600/60000(21%)] ，loss：0.1318 ，训练正确率：97.68% ，校验正确率：97.44000244140625%
训练周期：16 [2400/60000(32%)] ，loss：0.0548 ，训练正确率：97.67% ，校验正确率：97.58000183105469%
训练周期：16 [3200/60000(43%)] ，loss：0.0341 ，训练正确率：97.64% ，校验正确率：97.66000366210938%
训练周期：16 [4000/60000(53%)] ，loss：0.0393 ，训练正确率：97.69% ，校验正确率：97.72000122070312%
训练周期：16 [4800/60000(64%)] ，loss：0.1236 ，训练正确率：97.70% ，校验正确率：97.66000366210938%
训练周期：16 [5600/60000(75%)] ，loss：0.0735 ，训练正确率：97.73% ，校验正确率：97.68000030517578%
训练周期：16 [6400/60000(85%)] ，loss：0.1422 ，训练正确率：97.75% ，校验正确率：97.54000091552734%
训练周期：16 [7200/60000(96%)] ，loss：0.0473 ，训练正确率：97.75% ，校验正确率：97.66000366210938%
训练周期：17 [0/60000(0%)] ，loss：0.0878 ，训练正确率：95.31% ，校验正确率：97.80000305175781%
训练周期：17 [800/60000(11%)] ，loss：0.1094 ，训练正确率：97.91% ，校验正确率：97.69999694824219%
训练周期：17 [1600/60000(21%)] ，loss：0.0232 ，训练正确率：97.94% ，校验正确率：97.77999877929688%
训练周期：17 [2400/60000(32%)] ，loss：0.0407 ，训练正确率：97.86% ，校验正确率：97.68000030517578%
训练周期：17 [3200/60000(43%)] ，loss：0.0325 ，训练正确率：97.83% ，校验正确率：97.77999877929688%
训练周期：17 [4000/60000(53%)] ，loss：0.0761 ，训练正确率：97.81% ，校验正确率：97.73999786376953%
训练周期：17 [4800/60000(64%)] ，loss：0.0362 ，训练正确率：97.87% ，校验正确率：97.86000061035156%
训练周期：17 [5600/60000(75%)] ，loss：0.1176 ，训练正确率：97.85% ，校验正确率：97.76000213623047%
训练周期：17 [6400/60000(85%)] ，loss：0.0301 ，训练正确率：97.84% ，校验正确率：97.5%
训练周期：17 [7200/60000(96%)] ，loss：0.0226 ，训练正确率：97.84% ，校验正确率：97.80000305175781%
训练周期：18 [0/60000(0%)] ，loss：0.0950 ，训练正确率：96.88% ，校验正确率：97.76000213623047%
训练周期：18 [800/60000(11%)] ，loss：0.0364 ，训练正确率：97.83% ，校验正确率：97.81999969482422%
训练周期：18 [1600/60000(21%)] ，loss：0.0629 ，训练正确率：97.78% ，校验正确率：97.73999786376953%
训练周期：18 [2400/60000(32%)] ，loss：0.0584 ，训练正确率：97.87% ，校验正确率：97.76000213623047%
训练周期：18 [3200/60000(43%)] ，loss：0.0140 ，训练正确率：97.90% ，校验正确率：97.73999786376953%
训练周期：18 [4000/60000(53%)] ，loss：0.0466 ，训练正确率：97.90% ，校验正确率：97.68000030517578%
训练周期：18 [4800/60000(64%)] ，loss：0.0474 ，训练正确率：97.89% ，校验正确率：97.62000274658203%
训练周期：18 [5600/60000(75%)] ，loss：0.0254 ，训练正确率：97.89% ，校验正确率：97.81999969482422%
训练周期：18 [6400/60000(85%)] ，loss：0.1784 ，训练正确率：97.87% ，校验正确率：97.87999725341797%
训练周期：18 [7200/60000(96%)] ，loss：0.0909 ，训练正确率：97.88% ，校验正确率：97.76000213623047%
训练周期：19 [0/60000(0%)] ，loss：0.0610 ，训练正确率：98.44% ，校验正确率：97.72000122070312%
训练周期：19 [800/60000(11%)] ，loss：0.0119 ，训练正确率：97.76% ，校验正确率：97.63999938964844%
训练周期：19 [1600/60000(21%)] ，loss：0.0104 ，训练正确率：97.90% ，校验正确率：97.72000122070312%
训练周期：19 [2400/60000(32%)] ，loss：0.0096 ，训练正确率：97.86% ，校验正确率：97.86000061035156%
训练周期：19 [3200/60000(43%)] ，loss：0.0829 ，训练正确率：97.91% ，校验正确率：98.0%
训练周期：19 [4000/60000(53%)] ，loss：0.1485 ，训练正确率：97.93% ，校验正确率：97.76000213623047%
训练周期：19 [4800/60000(64%)] ，loss：0.0753 ，训练正确率：97.95% ，校验正确率：97.87999725341797%
训练周期：19 [5600/60000(75%)] ，loss：0.1232 ，训练正确率：97.94% ，校验正确率：98.08000183105469%
训练周期：19 [6400/60000(85%)] ，loss：0.0367 ，训练正确率：97.95% ，校验正确率：97.9000015258789%
训练周期：19 [7200/60000(96%)] ，loss：0.1007 ，训练正确率：97.94% ，校验正确率：98.0%5. 测试模型
我们还可以尝试用训练过的模型在测试集上做测验，发现准确率可以达到99%
# 去除警告
import warnings
warnings.filterwarnings("ignore")# 在测试集上分批运行，并计算总的正确率
net.eval() #标志着模型当前为运行阶段
vals = [] #记录准确率所用列表
# 对测试数据进行循环
for data, target in test_loader:
data, target = Variable(data, volatile=True), Variable(target)
output = net(data) #将特征数据输入网络，得到分类的输出
val = rightness(output, target) #获得正确样本数以及总样本数
vals.append(val) #记录结果
# 计算准确率
rights = (sum([tup[0] for tup in vals]), sum([tup[1] for tup in vals]))
right_rate = 1.0 * rights[0] / rights[1]
right_ratetensor(0.9912)
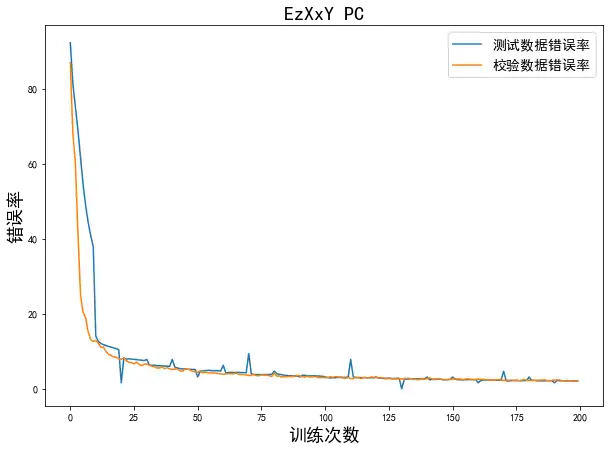
打印训练过程中的误差曲线
# 将 record 转化为 array 数组
record1 = np.asarray(record) #record记载了每一个打印周期记录的训练集和校验集上的准确度
# 绘制训练过程的误差曲线，校验集和测试集上的错误率
plt.figure(figsize=(10, 7))
xplot, = plt.plot(record1[:,0]) #绘制测试数据错误率曲线
yplot, = plt.plot(record1[:,1]) #绘制校验数据错误率曲线
# 显示中文
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
plt.xlabel('训练次数', size=18)
plt.ylabel('错误率', size=18)
plt.legend([xplot,yplot], ['测试数据错误率', '校验数据错误率'], prop={'size':14}) #绘制图例
plt.title('EzXxY PC', size=20)
6. 剖析卷积神经网络
让我们关注一下如下4个问题
- 1.第一层卷积核训练得到了什么？
- 2.在输入特定图像的时候，第一层卷积核所对应的 4 个特征图是什么样的？
- 3.第二层卷积核都是什么？
- 4.对于给定的输入图像，第二层卷积核所对应的特征图是什么样的？
6-1. 第一层卷积核与特征图
在之前对ConvNet的定义中，我们将第一层ConvNet定义成 4 个输出通道，使用了4个不同的卷积核，输出4个特征图作为第一层的输出。
# 提取第一层卷积层的卷积核
plt.figure(figsize=(10, 7))
for i in range(4):
plt.subplot(1, 4, i+1)
# 提取第一层卷积核中的权重值，注意 conv1 是 net 的属性
plt.imshow(net.conv1.weight.data.numpy()[i,0,...]) 
这些格子有着不同的数值和方块，就是我们第一层训练出来的卷积核，它们互不相同，但是我们并不能读懂这些卷积核的内容，需要结合每个卷积核对应的特征图才能更好地解读。
当输入图像6之后，我们可以将上述4个卷积核对应的4张特征图打印出来。
# 调用 net 的 retrieve_features 方法可以抽取出输入当前数据后输出的所有特征图（第一个卷积层和第二个卷积层）
# 首先定义接入的图片，它是从 test_dataset 中提取第 idx 个批次的第 0 个图
# 其次 unsqueeze 的作用是在最前面添加一维
# 目的是让这个 input_x 的 tensor 是四维的，这样才能输入给 net 。补充的那一维表示 batch
input_x = test_dataset[idx][0].unsqueeze(0)
# feature_maps 是有两个元素的列表，分别表示第一层和第二层卷积的所有特征图
feature_maps = net.retrieve_features(Variable(input_x))
plt.figure(figsize=(10,7))
# 打印出 4 个特征图
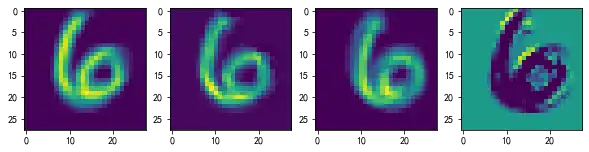
for i in range(4):
plt.subplot(1, 4, i+1)
plt.imshow(feature_maps[0][0, i, ...].data.numpy()) 
从第一层的特征图可以看到，有些卷积核会对图像做模糊化处理，如果熟悉计算机视觉的话，就会知道均值滤波可以达到这样的效果；有些卷积核会强化边缘并提取，对应经典的Gabor滤波或者Sabel滤波。由此可见，我们的卷积核确实可以通过对样本的学习具备提取边缘的能力，从而实现一些传统计算机视觉中经典算法的效果。
6-2. 第二层卷积核与特征图
类似地，我们可以对第二层所有的卷积核进行可视化
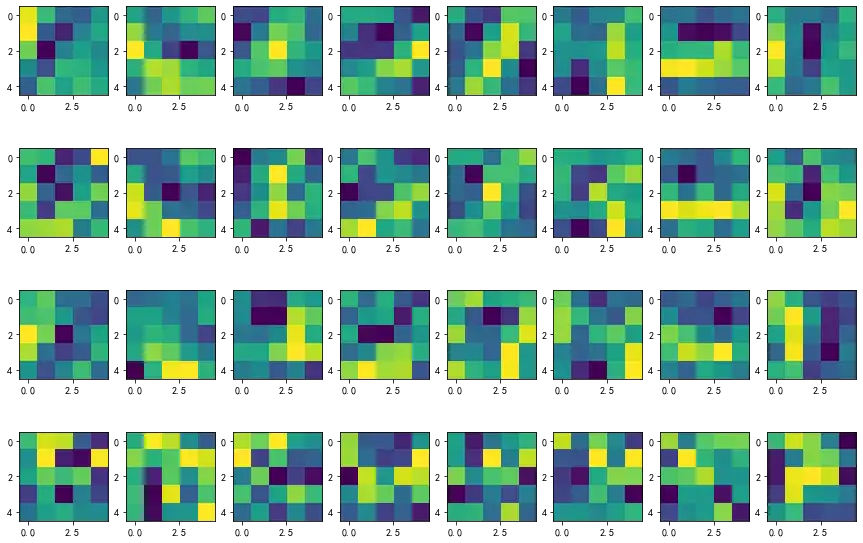
# 绘制第二鞥的卷积核，每一列对应一个卷积核，一共有 8 个卷积核
plt.figure(figsize=(15,10))
for i in range(4):
for j in range(8):
plt.subplot(4, 8, i * 8 + j + 1)
plt.imshow(net.conv2.weight.data.numpy()[j, i, ...]) 
图中每一列为一个卷积核，（注意，由于第二层卷积层的输入尺寸是(4,28,28)，所以每个卷积核是一个(4,5,5)的张量）。第二层一共有8个卷积核，因此一共有8列。接下来绘制在输入手写数字6之后第二层的特征图。
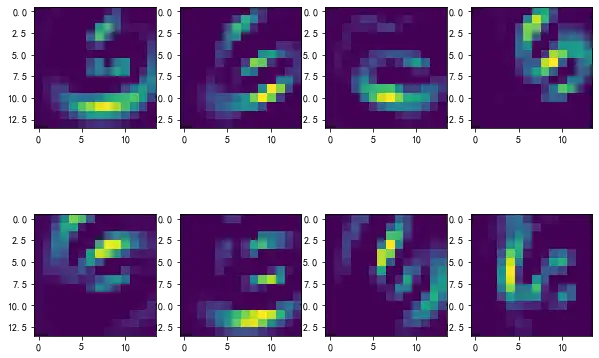
# 绘制第二层的特征图，一共有 8 个
plt.figure(figsize=(10, 7))
for i in range(8):
plt.subplot(2, 4, i + 1)
plt.imshow(feature_maps[1][0, i, ...].data.numpy())
数字6的第二层特征图表现得更加抽象了，这个简单的多层神经网络已经学习到了提取手写数字的抽象特征能力，它能将数字图像进行平移、旋转、聚合、打散，为后续的分类前馈神经网络提供足够多的特征值。
7. 小结
① PyTorch自带的数据集、数据加载器和采样器
torchvision.dataset.MNIST()——下载 & 加载 MNIST 测试数据集；
torch.utils.data.DataLoader()——加载 MNIST 训练数据集、根据采样器定义加载器。
torch.utils.data.sampler.SubsetRandomSampler()——对数据集的下标进行采样。
torch.utils.data.DataLoader()——加载 MNIST 训练数据集、根据采样器定义加载器。
torch.utils.data.sampler.SubsetRandomSampler()——对数据集的下标进行采样。
② 防止过拟合的dropout技术
“随机”关闭一些神经元，每次训练不同的神经网络，以提高每个单一神经元的强度。
③ 各层提取出的特征图
实现传统计算机视觉中经典算法的效果；
多层卷积网络具有很强的抽象提取能力。
多层卷积网络具有很强的抽象提取能力。
